题目内容
设a=
,b=p
,c=x+y,若对任意正实数x,y都存在以a,b,c为三边的三角形,则实数p的取值范围是( )
| x2-xy+y2 |
| xy |
| A、(1,3) |
| B、(0,1)∪(3,+∞) |
| C、(2,4) |
| D、(2,3) |
考点:基本不等式
专题:不等式的解法及应用
分析:由基本不等式可得a≥
,c≥2
,由三角形任意两边之和大于第三边可得关于p的不等式组,解不等式组可得.
| xy |
| xy |
解答:
解:∵a=
≥
=
,
b=p
,c=x+y≥2
,
∵三角形任意两边之和大于第三边,
∴
+2
≥p
,p
+
≥2
且p
+2
≥
,
解得 1<p<3,故实数p的取值范围是(1,3),
故选:A
| x2-xy+y2 |
| 2xy-xy |
| xy |
b=p
| xy |
| xy |
∵三角形任意两边之和大于第三边,
∴
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
解得 1<p<3,故实数p的取值范围是(1,3),
故选:A
点评:本题考查基本不等式以及三角形中任意两边之和大于第三边,属基础题.

练习册系列答案
相关题目
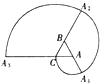 如图,一条螺旋线是用以下方法画成的:△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3是分别以A、B、C为圆心,AC、BA1、CA2为半径画的圆弧,曲线CA1A2A3称为螺旋线的第一圈,然后又以A为圆心,AA3为半径画圆弧…这样画到第n圈,则所得螺旋线的长度ln为( )
如图,一条螺旋线是用以下方法画成的:△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3是分别以A、B、C为圆心,AC、BA1、CA2为半径画的圆弧,曲线CA1A2A3称为螺旋线的第一圈,然后又以A为圆心,AA3为半径画圆弧…这样画到第n圈,则所得螺旋线的长度ln为( )| A、(3n2+n)π | ||
| B、(3n2-n+1)π | ||
C、
| ||
D、
|
已知函数f(x)=x2的图象上一点(1,1)及邻近一点(1+△x,1+△y),则
等于( )
| △y |
| △x |
| A、2 |
| B、2+△x |
| C、2+2△x |
| D、2△x+(△x)2 |
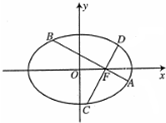 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆