题目内容
已知函数f（x）=x3-ax2-bx的图象与x轴相切于点（1，0），f（x）的极大值为 ．
考点：利用导数研究函数的极值
专题：导数的概念及应用
分析：根据相切，求出a，b，画出草图，得出结果．
解答：
解：（1，0）代入得1-a-b=0，
又f'（x）=3x2-2ax-b，
∴f'（1）=3-2a-b=0，
∴a=2，b=-1，
∴f（x）=x3-2x2+x，f'（x）=3x2-4x+1=（3x-1）（x-1），
∴f（x）极大值=f（
）=
．
故答案为
．
又f'（x）=3x2-2ax-b，
∴f'（1）=3-2a-b=0，
∴a=2，b=-1，
∴f（x）=x3-2x2+x，f'（x）=3x2-4x+1=（3x-1）（x-1），
∴f（x）极大值=f（
| 1 |
| 3 |
| 4 |
| 27 |
故答案为
| 4 |
| 27 |
点评：本题主要考查导数，切线极值 知识，属于基础知识，基本运算的考查
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
设a=
，b=p
，c=x+y，若对任意正实数x，y都存在以a，b，c为三边的三角形，则实数p的取值范围是（ ）
| x2-xy+y2 |
| xy |
| A、（1，3） |
| B、（0，1）∪（3，+∞） |
| C、（2，4） |
| D、（2，3） |
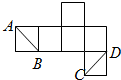
如图是正方体的平面展开图，则在这个正方体中AB与CD的位置关系为（ ）
| A、平行 |
| B、相交成60°角 |
| C、异面且垂直 |
| D、异面且成60°角 |
双曲线
-y2=1的焦点到渐近线的距离为（ ）
| x2 |
| m |
A、
| ||
B、
| ||
| C、1 | ||
D、
|