题目内容
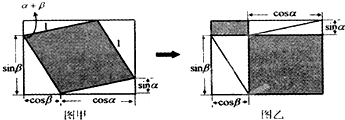
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用图甲、图乙中阴影部分的面积关系,写出该图所验证的一个三角恒等变换公式: .

考点:进行简单的合情推理
专题:计算题,推理和证明
分析:左右图中大矩形的面积相等,左边的图中阴影部分的面积为 S1=sin(α+β),在右边的图中,阴影部分的面积 S2 等于2个阴影小矩形的面积之和,等于sinαcosβ+cosαsinβ.而面积 S2 还等于大矩形得面积S 减去2个小空白矩形的面积,再由2个图中空白部分的面积相等,可得S1 =S2 ,从而得出结论.
解答:
解:在左边的图中大矩形的面积S=(cosβ+cosα)(sinβ+sinα)
=sinβcosβ+cosβsinα++sinβcosα+sinαcosα=sin(α+β)+sinβcosβ+sinαcosα.
用大矩形的面积S减去4个直角三角形的面积就等于阴影部分的面积 S1 .
空白部分的面积等于4个直角三角形的面积,即2×(
sinβcosβ+
sinαcosα)=sinβcosβ+sinαcosα.
故阴影部分的面积 S1 =S-sinβcosβ-sinαcosα=sin(α+β).
而在右边的图中阴影部分的面积 S2 等于2个阴影小矩形的面积之和,即S2=sinαcosβ+cosαsinβ.
在右边的图中大矩形的面积也等于S,S2等于大矩形得面积S 减去2个小空白矩形的面积,
而2个空白矩形的面积之和,即sinβcosβ+sinαcosα,
故左图中空白部分的面积等于右图中空白部分的面积.
故左右图中阴影部分的面积也相等,即 S1 =S2 ,故有sin(α+β)=sinαcosβ+cosαsinβ,
故答案为 sin(α+β)=sinαcosβ+cosαsinβ.
=sinβcosβ+cosβsinα++sinβcosα+sinαcosα=sin(α+β)+sinβcosβ+sinαcosα.
用大矩形的面积S减去4个直角三角形的面积就等于阴影部分的面积 S1 .
空白部分的面积等于4个直角三角形的面积,即2×(
| 1 |
| 2 |
| 1 |
| 2 |
故阴影部分的面积 S1 =S-sinβcosβ-sinαcosα=sin(α+β).
而在右边的图中阴影部分的面积 S2 等于2个阴影小矩形的面积之和,即S2=sinαcosβ+cosαsinβ.
在右边的图中大矩形的面积也等于S,S2等于大矩形得面积S 减去2个小空白矩形的面积,
而2个空白矩形的面积之和,即sinβcosβ+sinαcosα,
故左图中空白部分的面积等于右图中空白部分的面积.
故左右图中阴影部分的面积也相等,即 S1 =S2 ,故有sin(α+β)=sinαcosβ+cosαsinβ,
故答案为 sin(α+β)=sinαcosβ+cosαsinβ.
点评:本题主要考查三角函数的恒等式的证明,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
设a=
,b=p
,c=x+y,若对任意正实数x,y都存在以a,b,c为三边的三角形,则实数p的取值范围是( )
| x2-xy+y2 |
| xy |
| A、(1,3) |
| B、(0,1)∪(3,+∞) |
| C、(2,4) |
| D、(2,3) |
如图是正方体的平面展开图,则在这个正方体中AB与CD的位置关系为( )
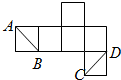

| A、平行 |
| B、相交成60°角 |
| C、异面且垂直 |
| D、异面且成60°角 |
双曲线
-y2=1的焦点到渐近线的距离为( )
| x2 |
| m |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
