题目内容
平面内给定三个向量
=(3,2),
=(-1,2),
=(4,1).
(Ⅰ)若(
+k
)∥(2
-
),求实数k的值;
(Ⅱ)设
=(x,y),且满足(
-
)⊥(
-
)且|
-
|=
,求
的值.
| a |
| b |
| c |
(Ⅰ)若(
| a |
| c |
| b |
| a |
(Ⅱ)设
| d |
| d |
| c |
| a |
| b |
| d |
| c |
| 5 |
| d |
考点:平面向量的综合题
专题:平面向量及应用
分析:(1)运用坐标表示的数量积解决.
(2)运用数量积和模求解.
(2)运用数量积和模求解.
解答:
解:(1)∵(
+k
)∥(2
-
),
=(3,2),
=(-1,2),
=(4,1).
∵
+k
=(3+4k,2+k),2
-
=(-5,2)
∴2×(3+4k)-(-5)×(2+k)=0
即k=-
(2)∵
-
=(x-4,y-1),
-
=(4,0)
又(
-
)⊥(
-
)且|
-
|=
∴
解得
或
∴
=(4,1+
)或
=(4,1+
)
| a |
| c |
| b |
| a |
| a |
| b |
| c |
∵
| a |
| c |
| b |
| a |
∴2×(3+4k)-(-5)×(2+k)=0
即k=-
| 16 |
| 13 |
(2)∵
| d |
| c |
| a |
| b |
又(
| d |
| c |
| a |
| b |
| d |
| c |
| 5 |
∴
|
|
|
∴
| d |
| 5 |
| d |
| 5 |
点评:本题考察了向量的数量积,向量的模的计算.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
直线l交椭圆
+
=1于A,B两点,若AB的中点为M=(2,1),则l的方程为( )
| x2 |
| 16 |
| y2 |
| 12 |
| A、2x-3y-1=0 |
| B、3x-2y-4=0 |
| C、2x+3y-7=0 |
| D、3x+2y-8=0 |
设a=
,b=p
,c=x+y,若对任意正实数x,y都存在以a,b,c为三边的三角形,则实数p的取值范围是( )
| x2-xy+y2 |
| xy |
| A、(1,3) |
| B、(0,1)∪(3,+∞) |
| C、(2,4) |
| D、(2,3) |
如图是正方体的平面展开图,则在这个正方体中AB与CD的位置关系为( )
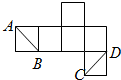

| A、平行 |
| B、相交成60°角 |
| C、异面且垂直 |
| D、异面且成60°角 |