题目内容
过双曲线
-
=1(a>0,b>0)的右焦点F和虚轴的一端点B作一条直线,若右顶点A到直线FB的距离为
,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| b | ||
|
A、
| ||||
| B、2 | ||||
C、2
| ||||
D、2或
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先根据三角形面积公式求得a,b和c的关系式,进而求得a和c的关系式,进而求得e.
解答:
解:∵S△ABF=
×
×|FB|=
b|AF|
∴
×
=(c-a)b
∴b2+c2=7(c-a)2
整理得5e2-14e+8=0,解得e=2
故选B.
| 1 |
| 2 |
| b | ||
|
| 1 |
| 2 |
∴
| b | ||
|
| b2+c2 |
∴b2+c2=7(c-a)2
整理得5e2-14e+8=0,解得e=2
故选B.
点评:本题主要考查了双曲线的简单性质.解题的关键是找到a和c的关系,进而求得双曲线的离心率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
α是第二象限角,P(x,
)为其终边上一点,cosα=
x,则sinα的值为( )
| 5 |
| ||
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
如果
<σ<
,那么下列不等式成立的是( )
| π |
| 4 |
| π |
| 2 |
| A、cosσ<sinσ<tanσ |
| B、tanσ<sinσ<cosσ |
| C、sinσ<cosσ<tanσ |
| D、cosσ<tanσ<sinσ |
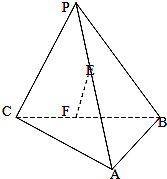 如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )| A、120° | B、45° |
| C、0° | D、60° |
如果函数y=3cos(2x+φ)的图象关于点(
,0)中心对称,那么ϕ的最小正值为( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|