题目内容
若直线y=kx+1与椭圆
+
=1恒有公共点,则m的取值范围是( )
| x2 |
| 2014 |
| y2 |
| m |
| A、[1,2014)∪(2014,+∞) |
| B、[1,2014) |
| C、[1,+∞) |
| D、(2014,+∞) |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:先根据直线方程可知直线恒过(0,1)点,要使直线y=kx+1与椭圆恒有公共点需(0,1)在椭圆上或椭圆内,进而求得m的范围.
解答:
解:直线y=kx+1恒过点(0,1),
∵直线y=kx+1与椭圆恒有公共点,
∴(0,1)在椭圆上或椭圆内,
∴0+
≤1,
解得m≥1
又m=2014时,曲线是圆不是椭圆,故m≠2014.
∴实数m的取值范围为:m≥1且m≠2014.
故选:A.
∵直线y=kx+1与椭圆恒有公共点,
∴(0,1)在椭圆上或椭圆内,
∴0+
| 1 |
| m |
解得m≥1
又m=2014时,曲线是圆不是椭圆,故m≠2014.
∴实数m的取值范围为:m≥1且m≠2014.
故选:A.
点评:本题主要考查了直线与圆锥曲线的综合问题,解答此题的关键在于明确直线过定点,是中档题.

练习册系列答案
相关题目
已知点P的极坐标是(2,π),则过点P且垂直极轴的直线方程是( )
| A、p=2 | ||
| B、p=2cosθ | ||
C、p=-
| ||
D、p=
|
某地铁的到站时间间隔是5分钟.某人进站到达列车门口等车时间超过2分钟的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在正三棱柱ABC-A1B1C1中,AA1=AB,F、F1分别是AC、A1C1的中点.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB,F、F1分别是AC、A1C1的中点.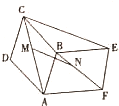 如图所示,ABCD-ABEF都是平行四边形,且不共面,M、N分别是AC、BF的中点,判断
如图所示,ABCD-ABEF都是平行四边形,且不共面,M、N分别是AC、BF的中点,判断