Question

已知x，y，a，b满足条件

x≥0，y≥0 a≥0，b≥0 2x+y+a=6 x+2y+b=6

．
（1）试画出点（x，y）的存在范围；
（2）求2x+3y的最大值．

Answer 1

考点：简单线性规划

专题：计算题,不等式的解法及应用

分析：（1）有x，y，a，b满足条件

x≥0，y≥0 a≥0，b≥0 2x+y+a=6 x+2y+b=6

，可得

x≥0，y≥0 -2x-y+6≥0 -x-2y+6≥0

，从而画出点（x，y）的存在范围；
（2）结合图形，可得在（2，2）处，2x+3y取得最大值．

解答： 解：（1）∵x，y，a，b满足条件

x≥0，y≥0 a≥0，b≥0 2x+y+a=6 x+2y+b=6

，
∴

x≥0，y≥0 -2x-y+6≥0 -x-2y+6≥0

，
可行域如图所示

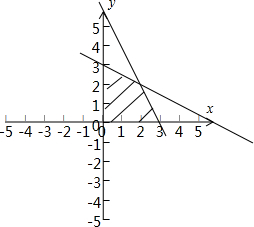
（2）由

-2x-y+6=0 -x-2y+6=0

，可得交点坐标为（2，2），
结合图形，可得在（2，2）处，2x+3y的最大值为10．

点评：本题主要考查了用线性规划的方法求最优解的问题，二元一次不等式表示平面区域，数形结合求函数最值的方法，转化化归的思想方法．