题目内容
14.若函数f(x)=2sinωx(ω>0)在区间$[{-\frac{π}{6}\;,\;\;\frac{π}{4}}]$上单调递增,则ω的最大值为2.且当ω取最大值时f(x)的值域为[-2,2].分析 根据三角函数的单调性的性质求出ω的值,结合三角函数的值域和单调性的关系进行求解即可.
解答 解:∵ω>0,
∴函数的周期T=$\frac{2π}{ω}$,则函数在[-$\frac{T}{4}$,$\frac{T}{4}$]上是增函数,
若f(x)在区间$[{-\frac{π}{6}\;,\;\;\frac{π}{4}}]$上单调递增,
则$\frac{π}{4}$≤$\frac{T}{4}$,即T≥π,即$\frac{2π}{ω}$≥π,则ω≤2,
则ω的最大值为2,
此时f(x)=2sin2x,则函数的最大值为2,最小值为-2,
即函数的值域为[-2,2],
故答案为:2,[-2,2]
点评 本题主要考查三角函数单调性和值域的求解,利用三角函数的周期公式以及三角函数单调性的性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
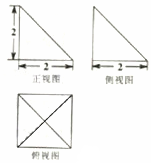

| A. | 4π | B. | 12π | C. | 48π | D. | 6$\sqrt{3}$π |
19.要得到函数$y=cos({2x-\frac{π}{3}})$的图象,只需将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
6.m,n表示两条不同直线,α,β,γ表示平面,下列说法正确的个数是( )
①若α∩β=m,α∩γ=n,且m∥n,则β∥γ;
②若m,n相交且都在α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;
③若α∩β=l,m∥α,m∥β,n∥α,n∥β,则m∥n;
④若m∥α,n∥α,则m∥n.
①若α∩β=m,α∩γ=n,且m∥n,则β∥γ;
②若m,n相交且都在α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;
③若α∩β=l,m∥α,m∥β,n∥α,n∥β,则m∥n;
④若m∥α,n∥α,则m∥n.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.设a=log310,b=log37,则3a-b=( )
| A. | $\frac{10}{49}$ | B. | $\frac{49}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{10}{7}$ |
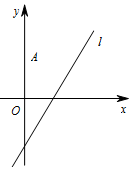 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=x-1,设圆C的半径为1,圆心在l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=x-1,设圆C的半径为1,圆心在l上. 如图所示的多面体ABCDE中,已知ABCD是边长为2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.
如图所示的多面体ABCDE中,已知ABCD是边长为2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.