题目内容
19.要得到函数$y=cos({2x-\frac{π}{3}})$的图象,只需将函数y=sin2x的图象( )| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
分析 先根据诱导公式化简可得y=sin[2(x+$\frac{π}{12}$)],再根据左加右减的原则进行平移从而可得到答案.
解答 解:∵$y=cos({2x-\frac{π}{3}})$=sin(2x+$\frac{π}{6}$)=sin[2(x+$\frac{π}{12}$)],
∴只需将函数y=sin2x的图象向左平移$\frac{π}{12}$个单位即可得到函数$y=cos({2x-\frac{π}{3}})$的图象.
故选:A.
点评 本题主要考查两角和与差的公式和三角函数的平移,三角函数平移时一定要遵循左加右减上加下减的原则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.某校校庆期间,大会秘书团计划从包括甲、乙两人在内的七名老师中随机选择4名参加志愿者服务工作,根据工作特点要求甲、乙两人中至少有1人参加,则甲、乙都被选中且列队服务时不相邻的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
9.函数y=cos 2x+2sin x的最大值为( )
| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
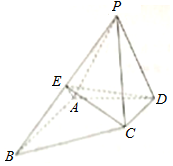 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点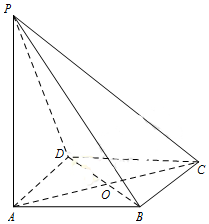 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.