题目内容
关于函数f(x)=|x2-1|,给出下列结论:
①f(x)是偶函数;
②若函数y=f(x)-m有四个零点,则实数m的取值范围是(0,1);
③f(x)在区间(0,+∞)内单调递增;
④若f(a)=f(b)(0<a<b),则0<ab<1.
其中正确的是( )
①f(x)是偶函数;
②若函数y=f(x)-m有四个零点,则实数m的取值范围是(0,1);
③f(x)在区间(0,+∞)内单调递增;
④若f(a)=f(b)(0<a<b),则0<ab<1.
其中正确的是( )
| A、①② | B、③④ |
| C、①③④ | D、①②④ |
考点:命题的真假判断与应用
专题:计算题,数形结合,函数的性质及应用
分析:作出函数f(x)=|x2-1|的图象,由奇偶性定义,可判断①;
作出直线y=m,由图象可知实数m的取值范围是(0,1),即可判断②;
由y轴右边的图象,可判断③;
若f(a)=f(b)(0<a<b),则a2+b2=2,a2+b2>2ab,即0<ab<1,即可判断④.
作出直线y=m,由图象可知实数m的取值范围是(0,1),即可判断②;
由y轴右边的图象,可判断③;
若f(a)=f(b)(0<a<b),则a2+b2=2,a2+b2>2ab,即0<ab<1,即可判断④.
解答:
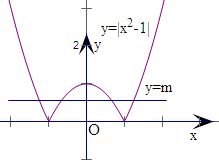 解:作出函数f(x)=|x2-1|的图象,
解:作出函数f(x)=|x2-1|的图象,
由f(-x)=f(x),可知f(x)是偶函数,故①正确;
若函数y=f(x)-m有四个零点,如图作出直线y=m,由图象可知
实数m的取值范围是(0,1),故②正确;
由图象可知,f(x)在(0,1)上递减,在(1,+∞)上递增,
故③错误;
若f(a)=f(b)(0<a<b),则1-a2=b2-1,即a2+b2=2,
a2+b2>2ab,即0<ab<1,故④正确.
故选:D.
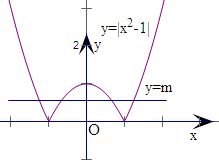 解:作出函数f(x)=|x2-1|的图象,
解:作出函数f(x)=|x2-1|的图象,由f(-x)=f(x),可知f(x)是偶函数,故①正确;
若函数y=f(x)-m有四个零点,如图作出直线y=m,由图象可知
实数m的取值范围是(0,1),故②正确;
由图象可知,f(x)在(0,1)上递减,在(1,+∞)上递增,
故③错误;
若f(a)=f(b)(0<a<b),则1-a2=b2-1,即a2+b2=2,
a2+b2>2ab,即0<ab<1,故④正确.
故选:D.
点评:本题考查函数的奇偶性、单调性和应用,考查数形结合的能力,注意运用图象求交点,判断函数的性质,属于中档题.

练习册系列答案
相关题目
随机变量ξ服从正态分布N(1,σ 2),已知P(ξ<0)=0.4,则P(ξ<2)=( )
| A、0.1 | B、0.2 |
| C、0.4 | D、0.6 |
若随机变量X服从两点分布,其中P(X=0)=
,则E(3X+2)和D(3X+2)的值分别是( )
| 1 |
| 3 |
| A、4和4 | B、4和2 |
| C、2和4 | D、2和2 |
a=0.90.9,b=0.93.1,c=0.9-1.5的大小关系是( )
| A、c<b<a |
| B、a<b<c |
| C、c<a<b |
| D、b<a<c |
函数y=-x2+2x-1,x∈(0,2]的( )
| A、最大值是0,最小值是-1 |
| B、最小值是0,无最大值 |
| C、最大值是1,最小值是0 |
| D、最大值是0,无最小值 |
圆(x-3)2+y2=1与圆(x-6)2+(y-4)2=36的位置关系是( )
| A、外离 | B、外切 | C、相交 | D、内切 |
将函数y=
cosx+sinx(x∈R)的图象向左平移
个长度单位后,所得到的图象关于( )对称.
| 3 |
| π |
| 6 |
| A、y轴 | ||
| B、原点(0,0) | ||
C、直线x=
| ||
D、点(
|
