题目内容
已知不等式-2x2+9x-4>0的解集为A.
(1)求集合A;
(2)对任意的x∈A,都使得不等式a-2x<
恒成立,求a的取值范围.
(1)求集合A;
(2)对任意的x∈A,都使得不等式a-2x<
| 4 |
| 2x-1 |
考点:二次函数的性质,函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:(1)不等式-2x2+9x-4>0可化为2x2-9x+4<0,即为(2x-1)(x-4)<0,解得答案;
(2)不等式a-2x<
可化为a<
+2x,由(1)中x的范围,结合基本不等式,可得a的取值范围.
(2)不等式a-2x<
| 4 |
| 2x-1 |
| 4 |
| 2x-1 |
解答:
解:(1)不等式-2x2+9x-4>0可化为2x2-9x+4<0
即为(2x-1)(x-4)<0
所以A={x|
<x<4}…(5分)
(2)不等式a-2x<
可化为a<
+2x…(7分)
因为
<x<4,所以0<2x-1<7
所以
+2x=
+2x-1+1≥2
+1=5…(10分)
(当且仅当x=
时等号成立)
所以a<5…(12分)
即为(2x-1)(x-4)<0
所以A={x|
| 1 |
| 2 |
(2)不等式a-2x<
| 4 |
| 2x-1 |
| 4 |
| 2x-1 |
因为
| 1 |
| 2 |
所以
| 4 |
| 2x-1 |
| 4 |
| 2x-1 |
| 4 |
(当且仅当x=
| 3 |
| 2 |
所以a<5…(12分)
点评:本题考查的知识点是二次函数的图象和性质,基本不等式,难度中档.

练习册系列答案
相关题目
已知函数f(x)的定义域为R,对任意实数m,n都满足 f(m+n)=f(m)+f(n)-1,当x>0时,f(x)>1,则不等式f(2x-1)+f(
)<2的解集是( )
| 1 |
| x |
A、(-∞,-
| ||
| B、(-∞,0) | ||
| C、(0,+∞) | ||
D、(-∞,-
|
f(x)=
的值域是( )
| 3x+1 |
| 3x+1 |
| A、(3,+∞) |
| B、(0,3) |
| C、(0,2) |
| D、(2,+∞) |
椭圆
+
=1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,下面结论正确的是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、P点有两个 |
| B、P点有四个 |
| C、P点不一定存在 |
| D、P点一定不存在 |
若直线(a2+4a+3)x+(a2+a-6)y-6=0与x-2y-1=0垂直,则a等于( )
| A、.5 | B、.5或-3 |
| C、.-3 | D、不存在 |
下列说法中错误的是( )
A、若f(x)=x2-3,g(x)=
| ||||||
| B、若函数的定义域只含有一个元素,则该函数的值域也只含有一个元素 | ||||||
| C、函数y=2x(x∈N)的图象是一条直线 | ||||||
D、y=
|
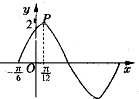 已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,
已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,