题目内容

O为平行四边形ABCD所在平面上一点，
OA
+
OB
=λ(
OC
+
OD
)，
OA
=μ(
AB
+2
AC
)，则λ的值是
 
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，分别取AB，CD的中点E，F，利用平行四边形法则可得
OA
+
OB
=2
OE
，
OC
+
OD
=2
OF
．由于
OA
+
OB
=λ(
OC
+
OD
)，可得
OE
=λ
OF
．作
AM
=2
AC
，以AM，AB为邻边作平行四边形ABNM．可得
AB
+2
AC
=
AN
．由于
OA
=μ(
AB
+2
AC
)，可得
OA
=μ
AN
．延长EF交直线MN与点P．利用平行线分线段成比例定理可得
OA
ON
=
AE
PN
=
FC
PN
=
1
2
，
OE
OP
=
AE
PN
=
1
4
=
OE
2OF
，即可得出．
解答： 解：如图所示，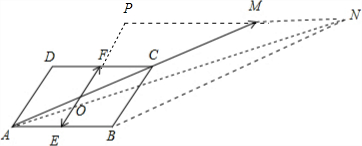
分别取AB，CD的中点E，F，
则
OA
+
OB
=2
OE
，
OC
+
OD
=2
OF
．
∵
OA
+
OB
=λ(
OC
+
OD
)，
∴
OE
=λ
OF
．
∴三点E，O，F共线．
作
AM
=2
AC
，
以AM，AB为邻边作平行四边形ABNM．
则
AB
+2
AC
=
AN
．
∵
OA
=μ(
AB
+2
AC
)，
∴
OA
=μ
AN
．
延长EF交直线MN与点P．
则
OA
ON
=
AE
PN
=
FC
PN
=
1
2
，
∴
OE
OP
=
AE
PN
=
1
4
=
OE
2OF
，
∴
OE
OF
=
1
2
．
∴λ=-
1
2
．
故答案为：-
1
2
．
点评：本题考查了向量的平行四边形法则、向量共线定理、平行线分线段成比例定理、平行四边形的性质，考查了作图能力，考查了推理能力与计算能力，属于难题．
练习册系列答案
相关题目
已知数列{an}满足an+1+an-1=2an（n∈N*，n≥2），且a3=7，a5+a7=26，{an}的前n项和为Sn．
（1）求an及Sn；
（2）令bn=
1
an2-1
（n∈N*），数列{bn}的前n项和Tn，求证Tn＜
1
4
．
已知
2x+y-2≥0
x-2y+4≥0
3x-y-3≤0
，
①当x，y取任何值时x2+y2取得最大值，并求最大值；
②当x，y取任何值时x2+y2取得最小值，并求最小值．
椭圆
x2
25
+
y2
16
=1的焦点是F1，F2，如果椭圆上一点P满足PF1⊥PF2，下面结论正确的是（　　）
A、P点有两个
B、P点有四个
C、P点不一定存在
D、P点一定不存在
若直线（a2+4a+3）x+（a2+a-6）y-6=0与x-2y-1=0垂直，则a等于（　　）
A、.5B、.5或-3
C、.-3D、不存在
已知f（x）是定义在R上的偶函数，当x∈[0，+∞）时，f（x）=2x-2，则不等式f（log2x）＞0的解集为（　　）
A、（0，
1
2
）
B、（
1
2
，1）∪（2，+∞）
C、（2，+∞）
D、（0，
1
2
）∪（2，+∞）
双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两焦点分别为F1，F2，以F1F2为边作等边三角形，若双曲线恰好平分三角形的两边，则此双曲线的离心率为
 
．
根据下列条件，写出直线的方程，并把它化成一般式：
（1）经过点A（8，-2），斜率是-
1
2
；
（2）经过点P1（3，-2），P2（5，-4）；
（3）在x轴，y轴上的截距分别是
3
2
，-3．
由函数y=ex，y=e及直线x=0所围成的图形的面积为（　　）
A、1
B、
1
2
e
C、e
D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网