题目内容
设{an}是集合{2s+2t|0≤s<t,且s,t∈Z}中所有的数从小到大排成的数列,则a50的值是( )
| A、1024 | B、1032 |
| C、1040 | D、1048 |
考点:数列的函数特性
专题:等差数列与等比数列
分析:由3=20+21,5=20+22,6=21+22,…,可得第i行的i个数是20+2i,21+2i,22+2i,…,2i-1+2i,(i∈N*)
设a50在第k行,解不等式1+2+3+…+k≥50,即
k(k+1)≥50,得满足条件的最小正整数k=10.a50在第10行第5个,即可得出.
设a50在第k行,解不等式1+2+3+…+k≥50,即
| 1 |
| 2 |
解答:
解:由3=20+21,
5=20+22,6=21+22,
9=20+23,10=21+23,3=22+23,
…
可得第i行的i个数是20+2i,21+2i,22+2i,…,2i-1+2i,(i∈N*)
设a50在第k行,解不等式1+2+3+…+k≥50,即
k(k+1)≥50,得满足条件的最小正整数k=10.
∴a50在第10行第5个,
∴a50=424+210=1040.
故选:C.
5=20+22,6=21+22,
9=20+23,10=21+23,3=22+23,
…
可得第i行的i个数是20+2i,21+2i,22+2i,…,2i-1+2i,(i∈N*)
设a50在第k行,解不等式1+2+3+…+k≥50,即
| 1 |
| 2 |
∴a50在第10行第5个,
∴a50=424+210=1040.
故选:C.
点评:本题考查了通过观察、分析、猜想、归纳求数列的通项公式的方法,考查了2的指数幂的运算性质,考查了推理能力和计算能力,属于难题.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=( )
| A、-1 | B、0 | C、1 | D、2 |
下述三个事件按顺序分别对应三个图象,正确的顺序是( )
①我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
②我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.
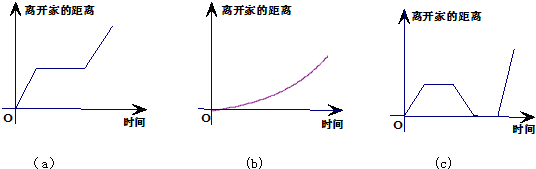
①我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
②我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.

| A、abc | B、bac |
| C、cab | D、acb |
已知复数z=
为纯虚数,则a的值为( )
| ai+1 |
| 1-i |
| A、-1 | B、1 | C、2 | D、-2 |
已知p>q>1,0<a<1,则下列各式中正确的是( )
| A、ap>aq |
| B、-pa>-qa |
| C、a-p>a-q |
| D、p-a>q-a |
已知命题p:“a<-
”是“函数f(x)=x2+4ax+1在区间(-∞,1)上是减函数”的充分不必要条件,命题q:a,b是任意实数,若a>b,则a2>b2.则( )
| 1 |
| 2 |
| A、“p且q”为真 |
| B、“p或q”为真 |
| C、p假q真 |
| D、p,q均为假命题 |
在极坐标系(ρ,θ)(0≤θ<2π)中,曲线ρ=2cosθ与ρsinθ=1的交点的极坐标是( )
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
