题目内容
下列函数中,以
为最小正周期的偶函数是( )
| π |
| 2 |
| A、y=sin2x+cos2x | ||
| B、y=sin2xcos2x | ||
C、y=cos(4x+
| ||
| D、y=sin22x-cos22x |
考点:三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:根据三角函数的奇偶性和周期性分别进行判断即可得到结论.
解答:
解:函数y=sin2x+cos2x=sin(2x+
)的周期为
=π,且为非奇非偶函数;
函数y=sin2xcos2x=
sin4x的周期为
=
,且为奇函数;
函数y=cos(4x+
)=sin4x的周期为
=
,且为奇函数;
函数y=sin22x-cos22x=-cos4x的周期为
=
,且为偶函数;
故选:D
| π |
| 4 |
| 2π |
| 2 |
函数y=sin2xcos2x=
| 1 |
| 2 |
| 2π |
| 4 |
| π |
| 2 |
函数y=cos(4x+
| π |
| 2 |
| 2π |
| 4 |
| π |
| 2 |
函数y=sin22x-cos22x=-cos4x的周期为
| 2π |
| 4 |
| π |
| 2 |
故选:D
点评:本题主要考查函数周期和奇偶性的判断,要求熟练掌握三角函数的图象和性质.

练习册系列答案
相关题目
下列表示方法正确的是( )
| A、0∈∅ | B、0∉∅ |
| C、0⊆∅ | D、0⊆∅ |
若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=( )
| A、-1 | B、0 | C、1 | D、2 |
设A={x|x-3≤4},B={y|y=
+
},则A∩B=( )
| x-2 |
| 2-x |
| A、{0} | B、{2} |
| C、∅ | D、{x|2≤x≤7} |
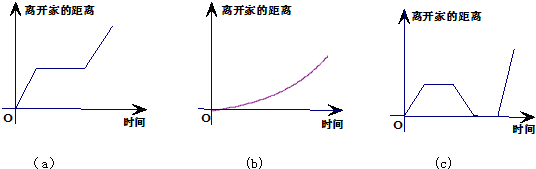
下述三个事件按顺序分别对应三个图象,正确的顺序是( )
①我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
②我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.
①我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
②我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.

| A、abc | B、bac |
| C、cab | D、acb |
已知复数z=
为纯虚数,则a的值为( )
| ai+1 |
| 1-i |
| A、-1 | B、1 | C、2 | D、-2 |
cos56°sin26°+cos34°cos154°=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|