题目内容
若关于x，y的不等式组
（k是常数）所表示的平面区域的边界是一个直角三角形，则k的值为（ ）
|
| A、0或1 | B、1或2 |
| C、0或2 | D、0或-1 |
考点：简单线性规划
专题：数形结合
分析：由约束条件作出可行域，根据直线kx-y+1=0恒过定点（0，1），数形结合得答案．
解答：
解：由约束条件作出可行域如图，
∵直线kx-y+1=0恒过定点（0，1），且不等式kx-y+1≥0表示的区域在直线kx-y+1=0的下方，
要使原不等式组所表示的平面区域的边界是直角三角形，
则有k=0或直线kx-y+1=0与y=x垂直，综上可得k=0或k=-1．
故选：D．
∵直线kx-y+1=0恒过定点（0，1），且不等式kx-y+1≥0表示的区域在直线kx-y+1=0的下方，
要使原不等式组所表示的平面区域的边界是直角三角形，
则有k=0或直线kx-y+1=0与y=x垂直，综上可得k=0或k=-1．
故选：D．
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
f（x）是偶函数，且f（x）在[0，+∞）上是增函数，不等式f（ax2+x+1）≤f（1）对x∈[
，1]恒成立，则实数a的取值范围是（ ）
| 1 |
| 2 |
| A、[-2，1] |
| B、[-3，0] |
| C、[-2，-1] |
| D、[-3，-2] |
函数f（x）=-x2+2 （a-1）x+2在区间（-∞，4）上递增，则a的取值范围是（ ）
| A、[-3，+∞） |
| B、（-∞，-3] |
| C、（-∞，5] |
| D、[5，+∞） |
若曲线y=kx+lnx在点（1，k）处的切线平行于x轴，则k=（ ）
| A、-1 | B、0 | C、1 | D、2 |
在数列{an}中，a1=2，2an+1-2an=1，则a101的值为（ ）
| A、49 | B、50 | C、51 | D、52 |
下述三个事件按顺序分别对应三个图象，正确的顺序是（ ）
①我离开家不久，发现自己把作业本忘在家里了，于是返回家里找到了作业本再上学；
②我骑着车一路匀速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；
③我出发后，心情轻松，缓慢行进，后来为了赶时间开始加速．
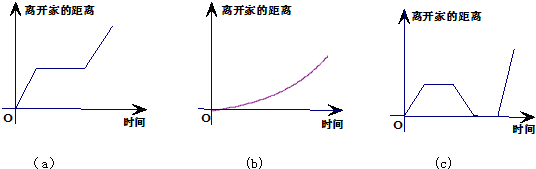
①我离开家不久，发现自己把作业本忘在家里了，于是返回家里找到了作业本再上学；
②我骑着车一路匀速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；
③我出发后，心情轻松，缓慢行进，后来为了赶时间开始加速．
| A、abc | B、bac |
| C、cab | D、acb |
已知p＞q＞1，0＜a＜1，则下列各式中正确的是（ ）
| A、ap＞aq |
| B、-pa＞-qa |
| C、a-p＞a-q |
| D、p-a＞q-a |
已知命题p：若x2-3x+2=0，则x=1；命题q：互斥事件一定是对立事件，则下列命题为真命题的是（ ）
| A、p∧q |
| B、p∧?q |
| C、p∨q |
| D、?p∨q |