题目内容
16.设a1=1,且an+1=3an+2•3n,(n∈N+),求an.分析 由数列递推式可得数列{$\frac{{a}_{n}}{{3}^{n}}$}是以$\frac{{a}_{1}}{3}=\frac{1}{3}$为首项,以$\frac{2}{3}$为公差的等差数列,求出等差数列的通项公式后可得an.
解答 解:由an+1=3an+2•3n,两边同时除以3n+1得:
$\frac{{a}_{n+1}}{{3}^{n+1}}=\frac{{a}_{n}}{{3}^{n}}+\frac{2}{3}$,即$\frac{{a}_{n+1}}{{3}^{n+1}}-\frac{{a}_{n}}{{3}^{n}}=\frac{2}{3}$.
∴数列{$\frac{{a}_{n}}{{3}^{n}}$}是以$\frac{{a}_{1}}{3}=\frac{1}{3}$为首项,以$\frac{2}{3}$为公差的等差数列,
则$\frac{{a}_{n}}{{3}^{n}}=\frac{1}{3}+\frac{2}{3}(n-1)=\frac{2}{3}n-\frac{1}{3}$,
∴${a}_{n}=(2n-1)•{3}^{n-1}$.
点评 本题考查数列递推式,考查了等差关系的确定,训练了等差数列通项公式的求法,是中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
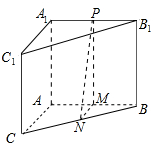 在三棱锥ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M,N,P分别是棱AB,BC,B1C1的中点.
在三棱锥ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M,N,P分别是棱AB,BC,B1C1的中点.