题目内容
有ABCDEFG共7人,想从7人中选出4名参加比赛,若A选中,B不选中,共有多少种不同的选法?
考点:计数原理的应用
专题:排列组合
分析:由题意,需要分三类,A选中,B选中,A不选中,B不选中,根据分类计数原理可得.
解答:
解:第一类:A选中,则有
=10种,
第二类,B选中,则有
=10种,
第三类,A不选中,B不选中,则有
=5种,
根据分类计数原理,共有10+10+5=25种不同选法.
故A选中,B不选中,共有25种不同的选法.
| C | 3 5 |
第二类,B选中,则有
| C | 3 5 |
第三类,A不选中,B不选中,则有
| C | 4 5 |
根据分类计数原理,共有10+10+5=25种不同选法.
故A选中,B不选中,共有25种不同的选法.
点评:本题主要考查了分类计数原理是,关键是如何分类,属于基础题.

练习册系列答案
相关题目
函数f(x)=(x-3)ex的单调递减区间是( )
| A、(-∞,2) |
| B、(0,3) |
| C、(1,4) |
| D、(2,+∞) |
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f′(x)≥0,则a=f(
),b=f(
),c=f(
)的大小关系是( )
| 16 |
| 3 |
| 17 |
| 3 |
| 23 |
| 3 |
| A、c<b<a |
| B、c<a<b |
| C、a<c<b |
| D、a<b<c |
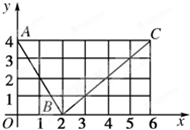 如图所示折线段ABC,其中A、B、C的坐标分别为(0,4),(2,0),(6,4).
如图所示折线段ABC,其中A、B、C的坐标分别为(0,4),(2,0),(6,4).