题目内容
已知双曲线方程为x2-4y2=16,则过点P(2,1)且与该双曲线只有一个公共点的直线有 条.
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:把直线与双曲线的位置关系,转化为方程组的解的个数来判断,借助判别式求解.注意分类讨论.
解答:
解;双曲线方程为x2-4y2=16,化为标准形式:
-
=1,
当k不存在时,直线为x=2,与
-
=1,无公共点,
当k存在时,直线为:y=k(x-2)+1,代入双曲线的方程可得:
(1-4k2)x2+(16k2-8k)x-16k2+16k-20=0,
(1)若1-4k2=0,k=
,时y=
x,所以无公共点,
k=-
时,y=-
x+2,与y=-
x平行,所以与双曲线只有1个公共点,
(2)k≠±
时,△=(16k2-8k)2-4×(1-4k2)(-16k2+16k-20)=-64k+80-192k2=0
即k=
(舍去),k=-
,此时直线y=-
(x-2)+1与双曲线相切,只有1个公共点.
综上过点P(2,1)且与该双曲线只有一个公共点的直线2条.
故答案为:2
| x2 |
| 16 |
| y2 |
| 4 |
当k不存在时,直线为x=2,与
| x2 |
| 16 |
| y2 |
| 4 |
当k存在时,直线为:y=k(x-2)+1,代入双曲线的方程可得:
(1-4k2)x2+(16k2-8k)x-16k2+16k-20=0,
(1)若1-4k2=0,k=
| 1 |
| 2 |
| 1 |
| 2 |
k=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)k≠±
| 1 |
| 2 |
即k=
| 1 |
| 2 |
| 5 |
| 6 |
| 5 |
| 6 |
综上过点P(2,1)且与该双曲线只有一个公共点的直线2条.
故答案为:2
点评:本题综合考查了直线与双曲线的位置关系,计算较复杂,化简运算要仔细认真.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
定义域为R的偶函数f(x)满足对任意x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,则a的取值范围是( )
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(0,
|
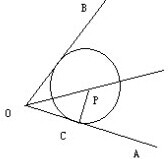 如图,点P是∠AOB平分线上一点,PC⊥OA,垂足为C,OB与以P为圆心、PC为半径的圆相切吗?为什么?
如图,点P是∠AOB平分线上一点,PC⊥OA,垂足为C,OB与以P为圆心、PC为半径的圆相切吗?为什么?