题目内容
在平面直角坐标系中,O为坐标原点,已知向量
=(2,1),A(1,0),B(cosθ,t).
(1)若
∥
,且|
|=
|
|,求向量
的坐标;
(2)若
∥
,求y=cos2θ-cosθ+t2的最小值.
| a |
(1)若
| a |
| AB |
| AB |
| 5 |
| OB |
| OB |
(2)若
| a |
| AB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)利用向量共线定理、模的计算公式即可得出;
(2)利用向量共线定理、二次函数的单调性即可得出.
(2)利用向量共线定理、二次函数的单调性即可得出.
解答:
解:(1)
=(cosθ-1,t).
∵
∥
,且|
|=
|
|,
∴
,
化为cosθ=0,t=-
.
∴
=(0,-
).
(2)∵
∥
,∴cosθ-1-2t=0.
∴cosθ=1+2t∈[-1,1],解得t∈[-1,0].
∴y=cos2θ-cosθ+t2=(1+2t)2-(1+2t)+t2=5t2+2t=5(t+
)2-
,
∵t∈[-1,0],∴当t=-
时,y取得最小值-
.
| AB |
∵
| a |
| AB |
| AB |
| 5 |
| OB |
∴
|
化为cosθ=0,t=-
| 1 |
| 2 |
∴
| OB |
| 1 |
| 2 |
(2)∵
| a |
| AB |
∴cosθ=1+2t∈[-1,1],解得t∈[-1,0].
∴y=cos2θ-cosθ+t2=(1+2t)2-(1+2t)+t2=5t2+2t=5(t+
| 1 |
| 5 |
| 1 |
| 5 |
∵t∈[-1,0],∴当t=-
| 1 |
| 5 |
| 1 |
| 5 |
点评:本题考查了向量共线定理、模的计算公式、二次函数的单调性,考查了计算能力,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
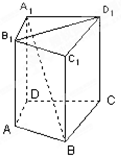 如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件
如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件