题目内容
7.曲线y=2xtanx在点x=$\frac{π}{4}$处的切线方程是(2+π)x-y-$\frac{{π}^{2}}{4}$=0.分析 根据求导公式(uv)′=u′v+uv′及x′=1和(tanx)′=sec2x,求出函数的导数,可得切线的斜率,进而求出切线的方程.
解答 解:y′=(2xtanx)′=2tanx+2xsec2x,
∴x=$\frac{π}{4}$,y′=2+π
∵y=$\frac{π}{2}$,
∴曲线y=2xtanx在点x=$\frac{π}{4}$处的切线方程是y-$\frac{π}{2}$=(2+π)(x-$\frac{π}{4}$),即(2+π)x-y-$\frac{{π}^{2}}{4}$=0.
故答案为(2+π)x-y-$\frac{{π}^{2}}{4}$=0.
点评 本题主要考查导数的几何意义,考查了导数的乘法法则,以及三角函数的导数,牢记求导公式是解本题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
15.已知$a={5^{{{log}_3}3.4}},b={5^{{{log}_4}3.6}},c={(\frac{1}{5})^{{{log}_3}0.3}}$,则( )
| A. | c>a>b | B. | b>a>c | C. | b>a>c | D. | a>c>b |
2.曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1与曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的( )
| A. | 实轴长相等 | B. | 离心率相等 | C. | 范围相同 | D. | 渐近线相同 |
12.设复数z满足(-1+3i)z=2(1+i),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.过圆C:(x-4)2+(y+1)2=25上的点M(0,2)作其切线l,且与直线l′:4x-ay+2=0平行,则l′与l间的距离是( )
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{28}{5}$ | D. | $\frac{12}{5}$ |
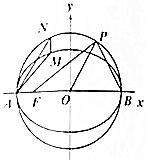 已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.
已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.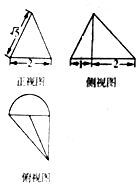 某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.
某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.