题目内容
8.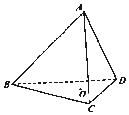 如图,在正四面体ABCD中,O是△BCD的中心,E,F分别是AB,AC上的动点,且$\overrightarrow{BE}$=λ$\overrightarrow{BA}$,$\overrightarrow{CF}$=(1-λ)$\overrightarrow{CA}$
如图,在正四面体ABCD中,O是△BCD的中心,E,F分别是AB,AC上的动点,且$\overrightarrow{BE}$=λ$\overrightarrow{BA}$,$\overrightarrow{CF}$=(1-λ)$\overrightarrow{CA}$(1)若OE∥平面ACD,求实数λ的值;
(2)若λ=$\frac{1}{2}$,正四面体ABCD的棱长为2$\sqrt{2}$,求平面DEF和平面BCD所成的角余弦值.
分析 (1)取CD的中点G,连接BG、AG,推导出点O在BG上,且$\frac{BO}{OG}=2$,当OE∥AG时,OE∥平面ACD,从而$\overrightarrow{BE}$=$\frac{2}{3}\overrightarrow{BA}$,由此能求出结果.
(2)当$λ=\frac{1}{2}$时,点E、F分别是AB、AC的中点.以O为原点,建立空间直角坐标系O-xyz,利用向量法能求出平面DEF和平面BCD所成的角的余弦值.
解答 解:(1)取CD的中点G,连接BG、AG,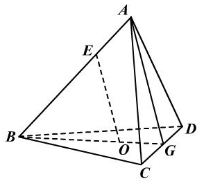
∵O是正△BCD的中心,∴点O在BG上,且$\frac{BO}{OG}=2$,
∵当OE∥AG时,OE∥平面ACD,
∴$\frac{BE}{EA}=\frac{BO}{OG}=2$,∴BE=$\frac{2}{3}BA$,即$\overrightarrow{BE}$=$\frac{2}{3}\overrightarrow{BA}$,
∵$\overrightarrow{BE}$=λ$\overrightarrow{BA}$,∴$λ=\frac{2}{3}$.
(2)当$λ=\frac{1}{2}$时,点E、F分别是AB、AC的中点.
以O为原点,建立如图所示的空间直角坐标系O-xyz,
依题设OB=2,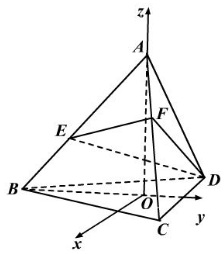
则B(0,-2,0),A(0,0,2$\sqrt{2}$),C($\sqrt{3},1,0$),
D(-$\sqrt{3},1,0$),
E(0,-1,$\sqrt{2}$),F($\frac{\sqrt{3}}{2},\frac{1}{2},\sqrt{2}$),
则$\overrightarrow{EF}$=($\frac{\sqrt{3}}{2},\frac{3}{2},0$),$\overrightarrow{DE}$=($\sqrt{3},-2,\sqrt{2}$),
设平面DEF的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=\sqrt{3}x-2y+\sqrt{2}z=0}\\{\overrightarrow{n}•\overrightarrow{EF}=\frac{\sqrt{3}}{2}x+\frac{3}{2}y=0}\end{array}\right.$,
令z=1,则$\overrightarrow{n}$=(-$\frac{\sqrt{6}}{5}$,$\frac{\sqrt{2}}{5}$,1),
又平面BCD的一个法向量为$\overrightarrow{m}$=(0,0,1).
设所求二面角为θ,则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{5\sqrt{33}}{33}$.
∴平面DEF和平面BCD所成的角的余弦值为$\frac{5\sqrt{33}}{33}$.
点评 本题考查满足条件的实数值的求法,考查二面角、空间中线线、线面、面面的位置关系等基础知识,考查推理论证能力、运算求解能力、空间思维能力,考查数形结合、化归与转化思想,是中档题.

 阅读快车系列答案
阅读快车系列答案| 价格x(百元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y(件/天) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)若以从这6天中随机抽取2天,至少有1天的价格高于700元的概率作为客户A,B购买此商品的概率,而客户C,D购买此商品的概率均为$\frac{1}{2}$,设这4位客户中购买此商品的人数为X,求X的分布列和数学期望.
参考数据:$\sum_{i=1}^{6}$xiyi=3050,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| A. | i | B. | -i | C. | -1 | D. | 1 |
| A. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$ | B. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{{\overrightarrow{a}}^{2}}$ | C. | $\frac{{\overrightarrow{b}}^{2}-{\overrightarrow{a}}^{2}}{|\overrightarrow{b}|}$ | D. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$ |
| A. | {m|-2≤m≤1} | B. | {m|-$\frac{1}{2}$≤m≤1} | C. | {m|-1≤m≤$\frac{1}{2}$} | D. | {m|-$\frac{1}{2}$≤m≤$\frac{1}{4}$} |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |