Question

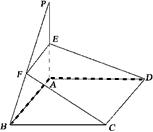如图，点P为矩形ABCD所在平面外一点，且PA⊥平面ABCD．
（1）求证：BC⊥平面PAB；
（2）过CD作一平面交平面PAB于EF．求证：CD∥EF．

Answer 1

考点：直线与平面垂直的判定,直线与平面平行的性质

专题：证明题,空间位置关系与距离

分析：（1）由ABCD是矩形可得BC⊥AB，又由PA⊥平面ABCD，BC⊥PA，AB∩AP=P，从而可证得BC⊥平面PAB．
（2）由CD∥AB且CD不在平面PAB上，可得CD∥平面PAB，又有EF?平面PAB，从而CD∥EF．

解答： 证明：（1）∵ABCD是矩形，∴BC⊥AB
又∵PA⊥平面ABCD，∴BC⊥PA，AB∩AP=P，
∴BC⊥平面PAB．
（2）∵CD∥AB且CD不在平面PAB上
∴CD∥平面PAB，
又∵EF?平面PAB，
∴CD∥EF．

点评：本题主要考查了直线与平面垂直的判定，直线与平面平行的性质，属于基本知识的考查．