题目内容
在等差数列{an}中,a1=13,前n项和为Sn,且S3=S11,则使得Sn最大的正整数n为 .
考点:等差数列的性质
专题:等差数列与等比数列
分析:由等差数列的求和公式可得公差d,进而可得通项公式,可得数列{an}的前7项均为正数,从第8项开始为负值,可得答案.
解答:
解:设等差数列{an}的公差为d,
∵a1=13,且S3=S11,
∴3×13+
d=11×13+
d,
解得d=-2,
∴an=13-2(n-1)=15-2n,
令15-2n≤0可解得n≥
,
∴等差数列{an}的前7项均为正数,从第8项开始为负值,
∴使得Sn最大的正整数n为7,
故答案为:7
∵a1=13,且S3=S11,
∴3×13+
| 3×2 |
| 2 |
| 11×10 |
| 2 |
解得d=-2,
∴an=13-2(n-1)=15-2n,
令15-2n≤0可解得n≥
| 15 |
| 2 |
∴等差数列{an}的前7项均为正数,从第8项开始为负值,
∴使得Sn最大的正整数n为7,
故答案为:7
点评:本题考查等差数列的性质,涉及等差数列的通项公式和求和公式,属基础题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
焦距为6,离心率e=
,焦点在x轴上的椭圆标准方程是( )
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=cosx•ln|x|的部分图象为( )
A、 |
B、 |
C、 |
D、 |
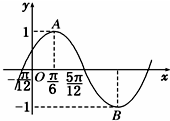 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
| A、y=sin 2x | ||
| B、y=cos 2x | ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
等轴双曲线的一个焦点是F1(-6,0),则它的标准方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
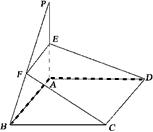 如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.
如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.