题目内容
已知sinα+sinβ=
,cosα-cosβ=
,求cos(α+β)的值.
| 1 |
| 2 |
| 1 |
| 3 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由已知条件,不易求得sinα,sinβ,cosα,cosβ.可将两式平方,整体构造出cos(α+β)求解.
解答:
解:由已知可得
sin2α+sin2β+2sinαsinβ=(
)2,
cos2α+cos2β-2cosαcosβ=
,
两式相加,2+2sinαsinβ-2cosαcosβ=
,
移向2sinαsinβ-2cosαcosβ=-
,
即2cos(α+β)=
,
所以cos(α+β)=
.
sin2α+sin2β+2sinαsinβ=(
| 1 |
| 2 |
cos2α+cos2β-2cosαcosβ=
| 1 |
| 9 |
两式相加,2+2sinαsinβ-2cosαcosβ=
| 13 |
| 36 |
移向2sinαsinβ-2cosαcosβ=-
| 59 |
| 36 |
即2cos(α+β)=
| 59 |
| 36 |
所以cos(α+β)=
| 59 |
| 72 |
点评:本题考查两角和与差的余弦函数,整体代换的方法.属于基本知识的考查.

练习册系列答案
相关题目
若等比数列{an}的前n项和为Sn,且S3=14,a1=2,则a4=( )
| A、16 | B、16或-16 |
| C、-54 | D、16或-54 |
焦距为6,离心率e=
,焦点在x轴上的椭圆标准方程是( )
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
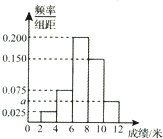 为了解某市今年八年级生的身体状况,从中抽取了一部份学生进行掷铅球的项目测试,成绩低于6米的为不合格,成绩在6至8米的(含6米不含8米)为及格,成绩在8至12米(含8米不含12米)为优秀.假定每个学生成绩均不超过12米.画出频率分布图如图.已知有4名学生的成绩在10米至12米之间.
为了解某市今年八年级生的身体状况,从中抽取了一部份学生进行掷铅球的项目测试,成绩低于6米的为不合格,成绩在6至8米的(含6米不含8米)为及格,成绩在8至12米(含8米不含12米)为优秀.假定每个学生成绩均不超过12米.画出频率分布图如图.已知有4名学生的成绩在10米至12米之间.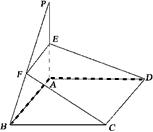 如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.
如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.