题目内容
已知f(x)=x2+ax+b,g(x)=x2+cx+d,又f(2x+1)=4g(x),且f′(x)=g′(x),f(5)=30,求g(2)的值.
考点:导数的运算
专题:导数的概念及应用
分析:因为f(2x+1)=4g(x),f′x=g′(x),f(5)=30得到四个式子联立求出a,b,c,d,即可求出g(2).
解答:
解:∵f(x)=x2+ax+b,g(x)=x2+cx+d,
∴由f(2x+1)=4g(x)得(4+2a-4c)x+1+a+b-4d=0,
即a-2c+2=0,a+b-4d+1=0;
又∵f′x=g′(x),得a=c,
又由f(5)=30,得5a+b=5,
四个方程联立求得:a=c=2,b=-5,d=-
则g(x)=x2+2x-
∴g(2)=4+4-
=
∴由f(2x+1)=4g(x)得(4+2a-4c)x+1+a+b-4d=0,
即a-2c+2=0,a+b-4d+1=0;
又∵f′x=g′(x),得a=c,
又由f(5)=30,得5a+b=5,
四个方程联立求得:a=c=2,b=-5,d=-
| 1 |
| 2 |
则g(x)=x2+2x-
| 1 |
| 2 |
∴g(2)=4+4-
| 1 |
| 2 |
| 15 |
| 2 |
点评:考查学生导数的运算能力,以及对函数值的运算能力.

练习册系列答案
相关题目
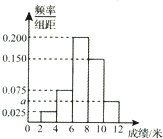 为了解某市今年八年级生的身体状况,从中抽取了一部份学生进行掷铅球的项目测试,成绩低于6米的为不合格,成绩在6至8米的(含6米不含8米)为及格,成绩在8至12米(含8米不含12米)为优秀.假定每个学生成绩均不超过12米.画出频率分布图如图.已知有4名学生的成绩在10米至12米之间.
为了解某市今年八年级生的身体状况,从中抽取了一部份学生进行掷铅球的项目测试,成绩低于6米的为不合格,成绩在6至8米的(含6米不含8米)为及格,成绩在8至12米(含8米不含12米)为优秀.假定每个学生成绩均不超过12米.画出频率分布图如图.已知有4名学生的成绩在10米至12米之间.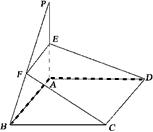 如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.
如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.