题目内容
已知数列{an}的前n项和Sn和通项公式an满足Sn=
(1-an)
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=nan,求Tn=b1+b2+…+bn的值.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=nan,求Tn=b1+b2+…+bn的值.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)首先利用前n项和公式证明数列是等比数列,进一步求出通项公式.
(2)利用(1)的结论求出新数列的通项,进一步利用乘公比错位相减法求数列的和.
(2)利用(1)的结论求出新数列的通项,进一步利用乘公比错位相减法求数列的和.
解答:
解:(1)当n≥2时,an=Sn-Sn-1=
(1-an)-
(1-an-1)
所以:3an=an-1
即:
=
所以数列{an}是以a1为首项,公比是
的等比数列.
当n=1时,求出s1=a1=
an=
•(
)n-1=
n
(2)由(1)知:bn=nan=n
n
所以:T=1×
+2×(
)2+…+n×(
)n①
Tn=1×(
)2+2×(
)3+…+n×(
)n+1②
①-②得:
Tn=
+(
)2+…+(
)n-n(
)n+1
解得:Tn=
-(
+n)(
)n+1
即:Tn=
-(
+
)(
)n
| 1 |
| 2 |
| 1 |
| 2 |
所以:3an=an-1
即:
| an |
| an-1 |
| 1 |
| 3 |
所以数列{an}是以a1为首项,公比是
| 1 |
| 3 |
当n=1时,求出s1=a1=
| 1 |
| 3 |
an=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)由(1)知:bn=nan=n
| 1 |
| 3 |
所以:T=1×
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
①-②得:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解得:Tn=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
即:Tn=
| 3 |
| 4 |
| 3 |
| 4 |
| n |
| 2 |
| 1 |
| 3 |
点评:本题考查的知识要点:利用前n项和公式求数列的通项公式,乘公比错位相减法的应用.属于基础题型.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
若等比数列{an}的前n项和为Sn,且S3=14,a1=2,则a4=( )
| A、16 | B、16或-16 |
| C、-54 | D、16或-54 |
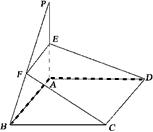 如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.
如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.