题目内容
设A、B、C、D是球面上的四点，AB、AC、AD两两互相垂直，且AB=3，AC=4，AD=
，则球的表面积为（ ）
| 11 |
| A、36π | B、64π |
| C、100π | D、144π |
考点：球的体积和表面积
专题：空间位置关系与距离
分析：以AB、AC、AD为棱长的长方体，内接于球，根据体对角线长为外接球的直径，得出半径，求解面积．
解答：
解：∵A、B、C、D是球面上的四点，AB、AC、AD两两互相垂直，且AB=3，AC=4，AD=
，
∴可以判断：以AB、AC、AD为棱长的长方体，
∴体对角线长为
=
=6，
外接球的直径为6，半径为3，
∴球的表面积为4π×32=36π，
故选：A
| 11 |
∴可以判断：以AB、AC、AD为棱长的长方体，
∴体对角线长为
| 32+42+11 |
| 36 |
外接球的直径为6，半径为3，
∴球的表面积为4π×32=36π，
故选：A
点评：本题考查了空间几何体的性质，运用求解体积，面积，属于中档题．
练习册系列答案
相关题目
已知点P（8，8）在抛物线C：y2=2px（p＞0）上，直线l与抛物线C相切于点P，则直线l的斜率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
数列{an}满足an+1+an=2n-3，若a1=2则a21-a20=（ ）
| A、9 | B、7 | C、5 | D、3 |
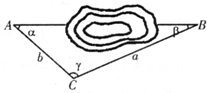如图，为了测量隧道两口之间AB的长度，对给出的四组数据，求解计算时，较为简便易行的一组是（ ）| A、a，b，γ |
| B、a，b，α |
| C、a，b，β |
| D、α，β，a |
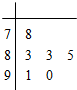对某同学的6次数学测试成绩（满分100分）进行统计，作出的茎叶图如图所示，给出关于该同学数学成绩的以下说法：