题目内容
已知函数f(x)=a lg(x2-2x+3)(a>0,a≠1)在R上有最小值2.
(1)求a的值;
(2)求f(x)的单调区间.
(1)求a的值;
(2)求f(x)的单调区间.
考点:复合函数的单调性
专题:函数的性质及应用
分析:(1)令t=x2-2x+3=(x-1)2+2,显然t>0恒成立,且t的最小值为2,t无最大值.根据题意可得a>1,且 alg2=2,由此求得a的值.
(2)由于f(x)=10t,故f(x)的单调增区间即函数t的增区间,f(x)的单调减区间即函数t的减区间,再结合二次函数t的性质可得结论.
(2)由于f(x)=10t,故f(x)的单调增区间即函数t的增区间,f(x)的单调减区间即函数t的减区间,再结合二次函数t的性质可得结论.
解答:
解:(1)令t=x2-2x+3=(x-1)2+2,显然t>0恒成立,且函数t在(-∞,1)上递减,在[1,+∞)上单调递增,
故t的最小值为2,t无最大值.
∵函数f(x)=a lg(x2-2x+3)=alg[(x-1)2+2] (a>0,a≠1)在R上有最小值2,
可得a>1,且 alg2=2,∴a=10.
(2)由于f(x)=at=10t,故f(x)的单调增区间即函数t的增区间,为[1,+∞);
f(x)的单调减区间即函数t的减区间,为(-∞,1).
故t的最小值为2,t无最大值.
∵函数f(x)=a lg(x2-2x+3)=alg[(x-1)2+2] (a>0,a≠1)在R上有最小值2,
可得a>1,且 alg2=2,∴a=10.
(2)由于f(x)=at=10t,故f(x)的单调增区间即函数t的增区间,为[1,+∞);
f(x)的单调减区间即函数t的减区间,为(-∞,1).
点评:本题主要考查复合函数的单调性,指数函数、二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知椭圆
+
=1上一点A(2,1)和该椭圆上两动点B、C,直线AB、AC的斜率分别为k1、k2,且k1+k2=0,则直线BC的斜率k( )
| x2 |
| 8 |
| y2 |
| 2 |
A、k>
| ||||
B、k=-
| ||||
C、k=
| ||||
| D、k的值不确定 |
设A、B、C、D是球面上的四点,AB、AC、AD两两互相垂直,且AB=3,AC=4,AD=
,则球的表面积为( )
| 11 |
| A、36π | B、64π |
| C、100π | D、144π |
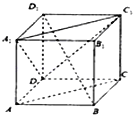 如图正方体ABCD-A1B1C1D1,下面结论正确的是
如图正方体ABCD-A1B1C1D1,下面结论正确的是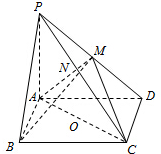 在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.
在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.