题目内容
已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=2
,E为CC1的中点,则直线BE与AC1所成角的余弦值为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线BE与AC1所成角的余弦值.
解答:
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,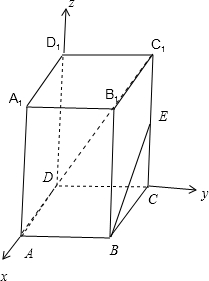
建立空间直角坐标系,
由已知得B(2,2,0),E(0,2,
),
A(2,0,0),C1(0,2,2
),
=(-2,0,
),
=(-2,2,2
),
|cos<
,
>|=|
|=
.
∴直线BE与AC1所成角的余弦值为
.
故选:D.

建立空间直角坐标系,
由已知得B(2,2,0),E(0,2,
| 2 |
A(2,0,0),C1(0,2,2
| 2 |
| BE |
| 2 |
| AC1 |
| 2 |
|cos<
| BE |
| AC1 |
| 4+0+4 | ||||
|
| ||
| 3 |
∴直线BE与AC1所成角的余弦值为
| ||
| 3 |
故选:D.
点评:本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={y|y=x2-2x+2,-1≤x≤2},B={x|
>1}},若任取x∈A,则x∈A∩B的概率为( )
| 2x-7 |
| x-3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在正方体ABCD-A′B′C′D′中,点P在线段AD′上运动,则异面直线CP与BA′所成的角θ的取值范围是( )
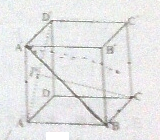

A、0<θ<
| ||
B、0<θ≤
| ||
C、0≤θ≤
| ||
D、0<θ≤
|
函数y=
的图象大致是( )
| x2 |
| ln|x| |
A、 |
B、 |
C、 |
D、 |
