题目内容
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知cos2A+
=2cosA.
(1)求角A的大小;
(2)若a=1,求△ABC的周长l的取值范围.
| 3 |
| 2 |
(1)求角A的大小;
(2)若a=1,求△ABC的周长l的取值范围.
考点:正弦定理,三角函数中的恒等变换应用
专题:计算题,三角函数的求值,解三角形
分析:(1)运用二倍角公式以及特殊角的三角函数值,即可得到A;
(2)运用正弦定理,求得b,c,再由两角差的正弦公式,结合正弦函数的图象和性质,即可得到范围.
(2)运用正弦定理,求得b,c,再由两角差的正弦公式,结合正弦函数的图象和性质,即可得到范围.
解答:
解:(1)cos2A+
=2cosA,
即2cos2A-1+
=2cosA,
即有4cos2A-4cosA+1=0,
(2cosA-1)2=0,
即cosA=
,(0<A<π),
则A=
;
(2)由正弦定理可得b=
=
=
sinB,
c=
=
sinC,
则l=a+b+c=1+
(sinB+sinC),
由A=
,B+C=
,
则sinB+sinC=sinB+sin(
-B)=
sinB+
cosB=
sin(B+
),
即有l=1+2sin(B+
),
由于0<B<
,则
<B+
<
,
<sin(B+
)≤1,
即有2<l≤3.
则有△ABC的周长l的取值范围为(2,3].
| 3 |
| 2 |
即2cos2A-1+
| 3 |
| 2 |
即有4cos2A-4cosA+1=0,
(2cosA-1)2=0,
即cosA=
| 1 |
| 2 |
则A=
| π |
| 3 |
(2)由正弦定理可得b=
| asinB |
| sinA |
| sinB | ||||
|
| 2 | ||
|
c=
| asinC |
| sinA |
| 2 | ||
|
则l=a+b+c=1+
| 2 | ||
|
由A=
| π |
| 3 |
| 2π |
| 3 |
则sinB+sinC=sinB+sin(
| 2π |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
即有l=1+2sin(B+
| π |
| 6 |
由于0<B<
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
即有2<l≤3.
则有△ABC的周长l的取值范围为(2,3].
点评:本题考查三角函数的化简和求值,考查正弦定理和二倍角公式及两角和差的正弦公式,考查正弦函数的图象和性质,考查运算能力,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
在正方体ABCD-A′B′C′D′中,点P在线段AD′上运动,则异面直线CP与BA′所成的角θ的取值范围是( )
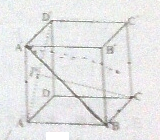

A、0<θ<
| ||
B、0<θ≤
| ||
C、0≤θ≤
| ||
D、0<θ≤
|
已知cos(60°+α)=
,且α为第三象限角,则cos(30°-α)+sin(30°-α)的值为( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=
的图象大致是( )
| x2 |
| ln|x| |
A、 |
B、 |
C、 |
D、 |
命题“若函数f(x)=logax(a>0,a≠1)在其定义域内是减函数,则loga2<0”的逆否命题是( )
| A、若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数 |
| B、若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数 |
| C、若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数 |
| D、若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数 |
已知x,y是两个具有线性相关关系的变量,现有这两个变量的十个样本点(x1,y1)(x2,y2),…,(x10,y10),同学甲利用最小二乘法得到回归直线l1:y=bx+a,同学乙将十个样本点中的两个点连起来得到拟合直线l2:y=dx+c,则下列判断一定正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
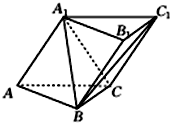 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.