题目内容
已知函数f(x)=Asin(
+φ)( A>0,0<φ<π)的最大值是2,且f(0)=2.
(1)求φ的值;
(2)设α,β∈[0,
],f(2α)=
,f(2β+π)=-
,求sin(α+β)的值.
| x |
| 2 |
(1)求φ的值;
(2)设α,β∈[0,
| π |
| 2 |
| 6 |
| 5 |
| 10 |
| 13 |
考点:正弦函数的图象,两角和与差的正弦函数,函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的求值
分析:(1)由函数f(x)的最大值是2,A>0可求得A=2,由f(0)=2及0<φ<π即可求得φ的值;
(2)先求得f(x)的解析式,由已知即可求得cosα=
,sinβ=
,从而可得sinα,cosβ,即可由两角和的正弦公式求sin(α+β)的值.
(2)先求得f(x)的解析式,由已知即可求得cosα=
| 3 |
| 5 |
| 5 |
| 13 |
解答:
解:(1)∵函数f(x)的最大值是2,A>0
∴A=2…(2分)
∵f(0)=2sinφ=2
∴sinφ=1…(3分)
又∵0<φ<π
∴φ=
…(4分)
(2)由(1)可知f(x)=2sin(
+
)=2cos
…(6分)
∵f(2α)=2cosα=
∴cosα=
…(7分)
∵f(2β+π)=2cos(β+
)=-2sinβ=-
∴sinβ=
…(8分)
∵α,β∈[0,
]
∴sinα=
=
=
,cosβ=
=
=
…(10分)
∴sin(α+β)=sinαcosβ+cosαsinβ…(11分)=
×
+
×
=
…(12分)
∴A=2…(2分)
∵f(0)=2sinφ=2
∴sinφ=1…(3分)
又∵0<φ<π
∴φ=
| π |
| 2 |
(2)由(1)可知f(x)=2sin(
| x |
| 2 |
| π |
| 2 |
| x |
| 2 |
∵f(2α)=2cosα=
| 6 |
| 5 |
∴cosα=
| 3 |
| 5 |
∵f(2β+π)=2cos(β+
| π |
| 2 |
| 10 |
| 13 |
∴sinβ=
| 5 |
| 13 |
∵α,β∈[0,
| π |
| 2 |
∴sinα=
| 1-cos2α |
1-(
|
| 4 |
| 5 |
| 1-sin2β |
1-(
|
| 12 |
| 13 |
∴sin(α+β)=sinαcosβ+cosαsinβ…(11分)=
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 63 |
| 65 |
点评:本题考查了两角和与差的正弦函数公式的应用,正弦函数的图象和性质,属于中档题.

练习册系列答案
相关题目
设集合S={x|x>2},T={x|x2-x-12≤0},则S∩T=( )
| A、[3,+∞) |
| B、[4,+∞) |
| C、(2,3] |
| D、(2,4] |
已知集合A={y|y=x2-2x+2,-1≤x≤2},B={x|
>1}},若任取x∈A,则x∈A∩B的概率为( )
| 2x-7 |
| x-3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在正方体ABCD-A′B′C′D′中,点P在线段AD′上运动,则异面直线CP与BA′所成的角θ的取值范围是( )
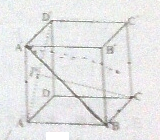

A、0<θ<
| ||
B、0<θ≤
| ||
C、0≤θ≤
| ||
D、0<θ≤
|

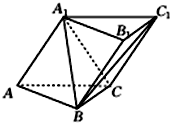 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.