题目内容
7.已知三角形的顶点是A(1,-1,1),B(2,1,-1),C(-1,-1,-2),则这个三角形的面积等于( )| A. | $\frac{\sqrt{101}}{2}$ | B. | $\frac{\sqrt{97}}{2}$ | C. | $\frac{\sqrt{103}}{2}$ | D. | $\frac{\sqrt{105}}{2}$ |
分析 由于S△ABC=$\frac{1}{2}$|AB||AC|sinα,其中α是AB与AC这两条边的夹角.只需要求出两边的长度,用向量求模公式可求,及两向量夹角的正弦,由数量积公式可求,由此三角形面积易求.
解答 解:S△ABC=$\frac{1}{2}$|AB||AC|sinα,其中α是AB与AC这两条边的夹角.则
S△ABC=$\frac{1}{2}$|$\overrightarrow{AB}$||$\overrightarrow{AC}$|$\sqrt{1-{cos}^{2}α}$=$\frac{1}{2}$|$\overrightarrow{AB}$||$\overrightarrow{AC}$|$\sqrt{1-(\frac{\overrightarrow{AB}•\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|\left|\overrightarrow{AC}\right|})^{2}}$=$\frac{1}{2}$$\sqrt{\left|\overrightarrow{AB}{|}^{2}\right|\overrightarrow{AC}{|}^{2}-(\overrightarrow{AB}{•\overrightarrow{AC})}^{2}}$.
∵$\overrightarrow{AB}$=(2,1,-1)-(1,-1,1)=(1,2,-2),
$\overrightarrow{AC}$=(-1,-1,-2)-(1,-1,1)=(-2,0,-3),
∴|$\overrightarrow{AB}$|2=12+22+(-2)2=9,
|$\overrightarrow{AC}$|2=(-2)2+02+(-3)2=13,$\overrightarrow{AB}$•$\overrightarrow{AC}$=1•(-2)+2•0+(-2)•(-3)=-2+6=4,
∴S△ABC=$\frac{1}{2}$$\sqrt{9×13-{4}^{2}}$=$\frac{\sqrt{101}}{2}$.
故选:A.
点评 本题考查空间向量求直线间的夹角与距离,利用向量的模求距离,求角是向量的重要运用.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案| A. | 6 | B. | 8 | C. | 4 | D. | 2 |
| A. | 向量$\overrightarrow{AB}$∥$\overrightarrow{CD}$就是$\overrightarrow{AB}$所在的直线平行于$\overrightarrow{CD}$所在的直线 | |
| B. | 共线向量是在一条直线上的向量 | |
| C. | 长度相等的向量叫做相等向量 | |
| D. | 零向量长度等于0 |
| A. | 10 | B. | 9 | C. | 6 | D. | 5 |
 如图,四棱锥E-ABCD中,平面ABE⊥平面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,底面ABCD是直角梯形,且AB∥CD,AB⊥BC,AB=2CD=2BC=2,
如图,四棱锥E-ABCD中,平面ABE⊥平面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,底面ABCD是直角梯形,且AB∥CD,AB⊥BC,AB=2CD=2BC=2,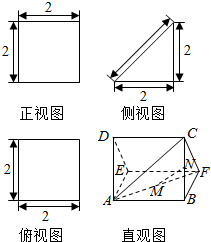 如图,多面体AED-BFC的直观图及三视图如图所示,M、N分别为AF、BC的中点.求证:
如图,多面体AED-BFC的直观图及三视图如图所示,M、N分别为AF、BC的中点.求证: