题目内容
15. 如图,四棱锥E-ABCD中,平面ABE⊥平面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,底面ABCD是直角梯形,且AB∥CD,AB⊥BC,AB=2CD=2BC=2,
如图,四棱锥E-ABCD中,平面ABE⊥平面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,底面ABCD是直角梯形,且AB∥CD,AB⊥BC,AB=2CD=2BC=2,(1)求证:AB⊥DE;
(2)求三棱锥C-BDE的体积;
(3)若点F是线段EA上一点,当EC∥平面FBD时,求EF的长.
分析 (1)取AB中点O,连结EO,DO.推出EO⊥AB.AB⊥BC,证明AB⊥平面EOD.即可证明AB⊥ED.
(2)利用体积转化VC-BDE=VE-CBD求解即可.
(3)连接AC、BD交于点,推出EC∥FM.通过△DMC与△BMA相似,然后求解EF即可.
解答 解:(1)证明:取AB中点O,连结EO,DO.
因为EB=EA,所以EO⊥AB.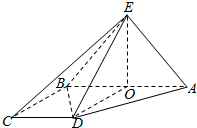
因为四边形ABCD为直角梯形,AB=2CD=2BC,AB⊥BC,
所以四边形OBCD为正方形,所以AB⊥OD.
所以AB⊥平面EOD.
所以 AB⊥ED.
(2)由EO⊥AB,面ABE⊥面ABCD,易得EO⊥ABCD,
所以,${V_{C-BDE}}={V_{E-CBD}}=\frac{1}{3}×(2×1×1)×1=\frac{1}{6}$.
(3)解:连接AC、BD交于点M,面ACE∩面FBD=FM.
因为EC∥平面FBD,所以EC∥FM.
在梯形ABCD中,有△DMC∽△BMA,可得MA=2MC,∴AF=2FE,
所以,$EF=\frac{1}{3}EA=\frac{{\sqrt{2}}}{3}$.
点评 本题考查几何体的体积的求法,平面与直线垂直判定定理以及性质定理定义域,直线与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力、转化思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.三条两两相交的直线最多可确定( )个平面.
| A. | 1 | B. | 2 | C. | 3 | D. | 无数 |
20.为了增强环保意识,我校从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
(Ⅰ)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(Ⅱ)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为$\frac{2}{3}$,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 总计 | |
| 男生 | 40 | 20 | 60 |
| 女生 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
(Ⅱ)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为$\frac{2}{3}$,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| k | 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
7.已知三角形的顶点是A(1,-1,1),B(2,1,-1),C(-1,-1,-2),则这个三角形的面积等于( )
| A. | $\frac{\sqrt{101}}{2}$ | B. | $\frac{\sqrt{97}}{2}$ | C. | $\frac{\sqrt{103}}{2}$ | D. | $\frac{\sqrt{105}}{2}$ |
 如图,长方体ABCD-A1B1C1D1中,AB=16,AD=10,AA1=6,点P在棱C1D1上,且D1P=6.
如图,长方体ABCD-A1B1C1D1中,AB=16,AD=10,AA1=6,点P在棱C1D1上,且D1P=6.