题目内容
17.抛物线x2=2py(p>0)的焦点F,其准线与双曲线$\frac{x^2}{3}-\frac{y^2}{3}=1$相交于A,B两点,若△ABC是等边三角形,则p等于( )| A. | 6 | B. | 8 | C. | 4 | D. | 2 |
分析 求出抛物线的焦点坐标,准线方程,然后求出抛物线的准线与双曲线的交点坐标,利用三角形是等边三角形求出p即可.
解答 解:抛物线的焦点坐标为(0,$\frac{p}{2}$),准线方程为:y=-$\frac{p}{2}$,
准线方程与双曲线联立解得x=±$\sqrt{3+\frac{{p}^{2}}{4}}$,
因为△ABF为等边三角形,所以p=$\frac{\sqrt{3}}{2}$•2$\sqrt{3+\frac{{p}^{2}}{4}}$,解得p=6.
故选:A.
点评 本题考查抛物线的简单性质,双曲线方程的应用,考查分析问题解决问题的能力以及计算能力.

练习册系列答案
相关题目
12.函数f(x)=ex-2x+1在[0,1)上的最小值是( )
| A. | 2 | B. | e-1 | C. | 3-2ln2 | D. | 2-2ln2 |
2.直线x+y-2=0与圆x2+y2-4y=0的位置关系是( )
| A. | 相交且过圆心 | B. | 相离 | C. | 相切 | D. | 相交且不过圆心 |
6.三条两两相交的直线最多可确定( )个平面.
| A. | 1 | B. | 2 | C. | 3 | D. | 无数 |
7.已知三角形的顶点是A(1,-1,1),B(2,1,-1),C(-1,-1,-2),则这个三角形的面积等于( )
| A. | $\frac{\sqrt{101}}{2}$ | B. | $\frac{\sqrt{97}}{2}$ | C. | $\frac{\sqrt{103}}{2}$ | D. | $\frac{\sqrt{105}}{2}$ |
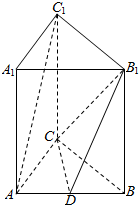 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,点D是AB的中点.