题目内容
2.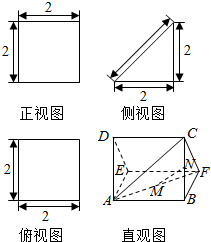 如图,多面体AED-BFC的直观图及三视图如图所示,M、N分别为AF、BC的中点.求证:
如图,多面体AED-BFC的直观图及三视图如图所示,M、N分别为AF、BC的中点.求证:(1)MN∥平面CDEF;
(2)CM⊥AF.
分析 (1)连结EB,则MN∥EC,由此能证明MN∥平面CDEF.
(2)由已知推导出EB⊥AF,从而AF⊥平面BCE,由此能证明CM⊥AF.
解答 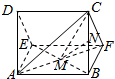 证明:(1)由多面体AED-BFC的三视图知,
证明:(1)由多面体AED-BFC的三视图知,
三棱柱AED-BFC中,底面DAE是等腰直角三角形,DA=AE=2,
DA⊥平面ABEF,侧面ABEF,ABCD都是边长为2的正方形,
连结EB,则M是EB的中点,
在△EBC中,MN∥EC,
∵EC?平面CDEF,MN?平面CDEF,
∴MN∥平面CDEF.
(2)∵DA⊥平面ABEF,DA∥BC,
BC⊥平面ABE,
∴BC⊥AF,
∵面ABEF是正方形,∴EB⊥AF,
∴AF⊥平面BCE,
∵AM?平面BCE,∴CM⊥AF.
点评 本题考查线面平行、线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
12.函数f(x)=ex-2x+1在[0,1)上的最小值是( )
| A. | 2 | B. | e-1 | C. | 3-2ln2 | D. | 2-2ln2 |
7.已知三角形的顶点是A(1,-1,1),B(2,1,-1),C(-1,-1,-2),则这个三角形的面积等于( )
| A. | $\frac{\sqrt{101}}{2}$ | B. | $\frac{\sqrt{97}}{2}$ | C. | $\frac{\sqrt{103}}{2}$ | D. | $\frac{\sqrt{105}}{2}$ |
12.函数y=ln(ax2+x-1)的值域为R,当且仅当( )
| A. | a≥0 | B. | a>0 | C. | a$≥-\frac{1}{4}$ | D. | a$<-\frac{1}{4}$ |
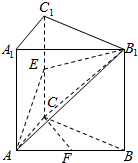 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.