题目内容
设数列{an}满足a1+
+
+…+
=2n,n∈N*.
(1)求数列{an}的通项公式;
(2)设bn=
,求数列{bn}的前n项和Sn.
| a2 |
| 2 |
| a3 |
| 22 |
| an |
| 2n-1 |
(1)求数列{an}的通项公式;
(2)设bn=
| an |
| (an-1)(an+1-1) |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用数列的前n项和与通项的关系可得an;
(2)利用“裂项求和”即可得出.
(2)利用“裂项求和”即可得出.
解答:
解:(1)∵a1+
+
+…+
=2n,n∈N*,①
∴当n=1时,a1=2.
当n≥2时,a1+
+
+…+
=2(n-1),②
①-②得,
=2.
∴an=2n.
a1=2,适合上式,
∴an=2n(n∈N*).
(2)由(1)得an=2n.
∴bn=
=
=
-
.
∴Sn=b1+b2+…+bn=(1-
)+(
-
)+(
-
)+…+(
-
)=1-
.
| a2 |
| 2 |
| a3 |
| 22 |
| an |
| 2n-1 |
∴当n=1时,a1=2.
当n≥2时,a1+
| a2 |
| 2 |
| a3 |
| 22 |
| an-1 |
| 2n-2 |
①-②得,
| an |
| 2n-1 |
∴an=2n.
a1=2,适合上式,
∴an=2n(n∈N*).
(2)由(1)得an=2n.
∴bn=
| an |
| (an-1)(an+1-1) |
| 2n |
| (2n-1)(2n+1-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
∴Sn=b1+b2+…+bn=(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 15 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
| 1 |
| 2n+1-1 |
点评:本题考查了数列的前n项和与通项的关系、“裂项求和”,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知自由落体运动的速率v=gt,则落体运动从t=0到t=t0所走的路程为( )
A、
| ||
| B、gt02 | ||
C、
| ||
D、
|
已知向量
=(1,1),
=(-1,0),λ
+μ
与
-2
共线,则
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| λ |
| μ |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
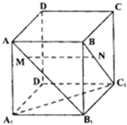 如图,正方体ABCD-A1B1C1D1棱长为1,点M∈AB1,N∈BC1,且AM=BN≠
如图,正方体ABCD-A1B1C1D1棱长为1,点M∈AB1,N∈BC1,且AM=BN≠