题目内容
某企业生产某种商品x吨,此时所需生产费用为(x2-100x+10000)万元,当出售这种商品时,每吨价格为p万元,这里p=ax+b(a,b为常数,x>0)
(1)为了使这种商品的生产费用平均每吨最低,那么这种商品的产量应为多少吨?
(2)如果生产出来的商品能全部卖完,当产量是120吨时企业利润最大,此时出售价格是每吨160万元,求a,b的值.
(1)为了使这种商品的生产费用平均每吨最低,那么这种商品的产量应为多少吨?
(2)如果生产出来的商品能全部卖完,当产量是120吨时企业利润最大,此时出售价格是每吨160万元,求a,b的值.
考点:函数模型的选择与应用
专题:
分析:(1)表示出商品的生产平均费用,利用基本不等式可求最值;
(2)设出售x吨时,利润是y元,根据售价-进价=利润列出关系式,利用二次函数与一次函数的性质列出关于a与b的方程,求出方程的解即可得到a与b的值.
(2)设出售x吨时,利润是y元,根据售价-进价=利润列出关系式,利用二次函数与一次函数的性质列出关于a与b的方程,求出方程的解即可得到a与b的值.
解答:
解:(1)商品的生产费用平均为
=x+
-100≥2
-100=100
当且仅当x=100时,取等号,
∴当产量x=100吨时,生产费用平均最低;
(2)设出售x吨时,利润是y元,
则根据题意有:y=(ax+b)x-(x2-100x+10000)
=(a-1)x2+(b+100)x-10000
=(a-1)[x+
]2-(a-1)[
]2-10000,
∵x=120时利润最大,
∴a-1<0,即a<1,-
=120,①
又160=120a+b,②
联立①②,解得:a=-
,b=180.
| x2-100x+10000 |
| x |
| 10000 |
| x |
x•
|
当且仅当x=100时,取等号,
∴当产量x=100吨时,生产费用平均最低;
(2)设出售x吨时,利润是y元,
则根据题意有:y=(ax+b)x-(x2-100x+10000)
=(a-1)x2+(b+100)x-10000
=(a-1)[x+
| b+100 |
| 2(a-1) |
| b+100 |
| 2(a-1) |
∵x=120时利润最大,
∴a-1<0,即a<1,-
| b+100 |
| 2(a-1) |
又160=120a+b,②
联立①②,解得:a=-
| 1 |
| 6 |
点评:本题考查利用数学知识解决实际问题,考查基本不等式的运用,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
某台体的三视图如图所示,则该台体的体积是( )


A、(5+
| ||
| B、28π | ||
| C、7π | ||
| D、21π |
已知自由落体运动的速率v=gt,则落体运动从t=0到t=t0所走的路程为( )
A、
| ||
| B、gt02 | ||
C、
| ||
D、
|
 某几何体的三视图如图所示,则该几何体的表面积是( )
某几何体的三视图如图所示,则该几何体的表面积是( )A、(2+
| ||
B、(4+
| ||
| C、4π | ||
| D、6π |
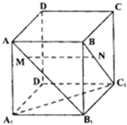 如图,正方体ABCD-A1B1C1D1棱长为1,点M∈AB1,N∈BC1,且AM=BN≠
如图,正方体ABCD-A1B1C1D1棱长为1,点M∈AB1,N∈BC1,且AM=BN≠