题目内容
以(-1,2)为圆心,
为半径的圆的方程为( )
| 5 |
| A、x2+y2-2x+4y=0 |
| B、x2+y2+2x+4y=0 |
| C、x2+y2+2x-4y=0 |
| D、x2+y2-2x-4y=0 |
考点:圆的一般方程
专题:直线与圆
分析:由圆心的坐标和半径写出圆的标准方程,再化为一般方程即可.
解答:
解:由圆心坐标为(-1,2),半径r=
,
则圆的标准方程为:(x+1)2+(y-2)2=5,
化为一般方程为:x2+y2+2x-4y=0.
故选C.
| 5 |
则圆的标准方程为:(x+1)2+(y-2)2=5,
化为一般方程为:x2+y2+2x-4y=0.
故选C.
点评:本题考查学生会根据圆心坐标和圆的半径写出圆的标准方程,是一道比较简单的题.要求学生掌握当圆心坐标为(a,b),半径为r时,圆的标准方程为(x-a)2+(y-b)2=r2.

练习册系列答案
相关题目
直线在平面外是指( )
| A、直线与平面没有公共点 |
| B、直线与平面相交 |
| C、直线与平面平行 |
| D、直线与平面最多只有一个公共点 |
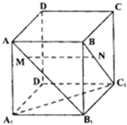 如图,正方体ABCD-A1B1C1D1棱长为1,点M∈AB1,N∈BC1,且AM=BN≠
如图,正方体ABCD-A1B1C1D1棱长为1,点M∈AB1,N∈BC1,且AM=BN≠