题目内容
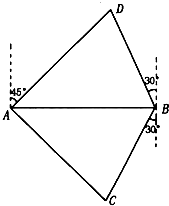如图，A，B是海面上位于东西方向相距5(| 3 |
| 7 |
考点：解三角形的实际应用
专题：解三角形
分析：在△DAB中，由正弦定理得
=
，由此可以求得DB，然后在△DBC中，由余弦定理得CD2=BD2+BC2-2BD•BC•cos∠DBC，求得CD；最后根据航行速度为10
海里/小时，即可求得该救援船到达D点需要的时间．
| BD |
| sin45° |
| AB |
| sin75° |
| 7 |
解答：
解：由题意，∠DAB=45°，∠DBA=60°，∴∠ADB=75°．
在△DAB中，由正弦定理得
=
，
∴BD=
•sin45°=
=10，
又∠DBC=∠DBA+∠ABC=120°，BC=20海里，
在△DBC中，由余弦定理得CD2=BD2+BC2-2BD•BC•cos∠DBC=100+400+200=700，
∴CD=10
，
∵航行速度为10
海里/小时，
∴该救援船到达D点需要
=1（小时）．
答：救援船到达D点需要1小时．
在△DAB中，由正弦定理得
| BD |
| sin45° |
| AB |
| sin75° |
∴BD=
| AB |
| sin75° |
5(
| ||||||||||
|
又∠DBC=∠DBA+∠ABC=120°，BC=20海里，
在△DBC中，由余弦定理得CD2=BD2+BC2-2BD•BC•cos∠DBC=100+400+200=700，
∴CD=10
| 7 |
∵航行速度为10
| 7 |
∴该救援船到达D点需要
| CD | ||
10
|
答：救援船到达D点需要1小时．
点评：本题考查了正弦定理与余弦定理，考查利用数学知识解决实际问题，准确找出题中的方向角是解题的关键之处．
练习册系列答案
相关题目
连掷两次骰子得到的点数分别为m和n，若记向量
=（m，n）与向量
=（1，-2）的夹角为θ，则θ为锐角的概率是（ ）
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|