题目内容
已知过抛物线y2=12x焦点的一条直线与抛物线相交于A，B两点，若|AB|=14，则线段AB的中点到y轴的距离等于（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
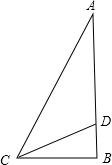
分析：设AB的中点为E，过 A、E、B 分别作准线的垂线，垂足分别为 C、G、D，如图所示，由EF为直角梯形的中位线及抛物线的定义求出EG，则 EH=EG-1 为所求．
解答：
解：抛物线y2=12x焦点（3，0），准线为 l：x=-3，
设AB的中点为E，过 A、E、B分别作准线的垂线，垂足分别为 C、G、D，EF交纵轴于点H，如图所示：
则由EF为直角梯形的中位线知，
EG=
=
=
=7，
∴EH=EG-3=4，
则AB的中点到y轴的距离等于4．
故选：D．
设AB的中点为E，过 A、E、B分别作准线的垂线，垂足分别为 C、G、D，EF交纵轴于点H，如图所示：
则由EF为直角梯形的中位线知，
EG=
| AC+BD |
| 2 |
| AF+BF |
| 2 |
| AB |
| 2 |
∴EH=EG-3=4，
则AB的中点到y轴的距离等于4．
故选：D．
点评：本题考查直线与抛物线的位置关系，抛物线的简单性质的应用，体现了数形结合的数学思想．
练习册系列答案
相关题目
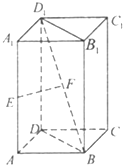如图，已知棱柱ABCD-A1B1C1D1的底面是正方形，且AA1⊥平面ABCD，E为棱AA1的中点，F为线段BD1的中点．
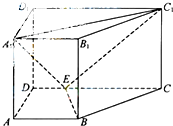如图，直四棱柱ABC-A1B1C1D1中，AB∥CD，AD⊥AB，AB=2，AD=