题目内容
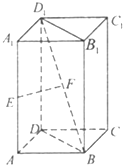 如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.
如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.(1)证明:EF∥平面ABCD;
(2)证明:EF⊥平面BB1D1D.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)根据中的找出平行线,利用判断定理证明.
(2)利用线线,线面,垂直的性质,判断定理转换求解.
(2)利用线线,线面,垂直的性质,判断定理转换求解.
解答:
 (14分)
(14分)
证明:(1)连接AC交BD与O,连接OF,
∵ABCD是正方形,
∴O是BD的中点,BD⊥OA,
又∵F为线段BD1的中点,
∴OF∥DD1且OF=
DD1,
∵E为棱AA1的中点,
∴OF∥AE且OF=AE,
∴EF∥OA,
∵OA?平面ABCD,且EF?平面ABCD,
∴EF∥平面ABCD,
(2)∵AA1⊥平面ABCD且AA1∥DD1,
∴DD1⊥平面ABCD,
∴DD1⊥OA,
∵BD⊥OA且BD?平面BB1D1D,D1D?平面BB1D1D,BD∩D1D=D,
∴OA⊥平面BB1D1D.
∵EF∥OA,
∴EF⊥平面BB1D1D.
 (14分)
(14分)证明:(1)连接AC交BD与O,连接OF,
∵ABCD是正方形,
∴O是BD的中点,BD⊥OA,
又∵F为线段BD1的中点,
∴OF∥DD1且OF=
| 1 |
| 2 |
∵E为棱AA1的中点,
∴OF∥AE且OF=AE,
∴EF∥OA,
∵OA?平面ABCD,且EF?平面ABCD,
∴EF∥平面ABCD,
(2)∵AA1⊥平面ABCD且AA1∥DD1,
∴DD1⊥平面ABCD,
∴DD1⊥OA,
∵BD⊥OA且BD?平面BB1D1D,D1D?平面BB1D1D,BD∩D1D=D,
∴OA⊥平面BB1D1D.
∵EF∥OA,
∴EF⊥平面BB1D1D.
点评:本题主要考查了直线与平面垂直的判定,考查了直线与平面平行的判定,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
某校开设A类课3门,B类课5门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有
( )
( )
| A、15种 | B、30种 |
| C、45种 | D、90种 |
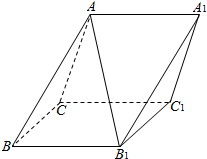 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.