题目内容
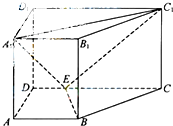 如图,直四棱柱ABC-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=
如图,直四棱柱ABC-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=| 2 |
(Ⅰ)证明:BE⊥平面BB1C1C;
(Ⅱ)求直线C1E与平面BB1C1C所成角的正弦值.
考点:直线与平面垂直的判定,直线与平面所成的角
专题:证明题,空间位置关系与距离
分析:(Ⅰ)过点B作BF⊥CD,垂足为F,可证在△BCE中,BE⊥BC,由BB1⊥平面ABCD,而BE?平面ABCD,可得BB1⊥BE,又BB1∩BC=B,即可证明BE⊥平面BB1C1C.
(Ⅱ) 连BC1,由BE⊥平面BB1C1C,可知∠BC1E是直线C1E与平面BB1C1C所成角,即可求解.
(Ⅱ) 连BC1,由BE⊥平面BB1C1C,可知∠BC1E是直线C1E与平面BB1C1C所成角,即可求解.
解答:
 证明:(Ⅰ)过点B作BF⊥CD,垂足为F,
证明:(Ⅰ)过点B作BF⊥CD,垂足为F,
则BF=AD=
,EF=AB-DE=1,FC=2,
在Rt△BFE中,BE=
,Rt△BFC中,BC=
.
在△BCE中,BE2+BC2=EC2,故BE⊥BC,
∵BB1⊥平面ABCD,而BE?平面ABCD,
∴BB1⊥BE,又BB1∩BC=B,
∴BE⊥平面BB1C1C.
(Ⅱ) 连BC1,∵BE⊥平面BB1C1C,
∴∠BC1E是直线C1E与平面BB1C1C所成角,
sin∠BC1E=
=
=
.
 证明:(Ⅰ)过点B作BF⊥CD,垂足为F,
证明:(Ⅰ)过点B作BF⊥CD,垂足为F,则BF=AD=
| 2 |
在Rt△BFE中,BE=
| 3 |
| 6 |
在△BCE中,BE2+BC2=EC2,故BE⊥BC,
∵BB1⊥平面ABCD,而BE?平面ABCD,
∴BB1⊥BE,又BB1∩BC=B,
∴BE⊥平面BB1C1C.
(Ⅱ) 连BC1,∵BE⊥平面BB1C1C,
∴∠BC1E是直线C1E与平面BB1C1C所成角,
sin∠BC1E=
| BE |
| EC1 |
| ||
3
|
| ||
| 6 |
点评:本题主要考查了直线与平面垂直的判定,考查了直线与平面所成角的正弦值的求法,属于中档题.

练习册系列答案
相关题目
函数f(x)=3x+x-2的零点所在的一个区间是( )
| A、(1,2) |
| B、(0,1) |
| C、(-2,-1) |
| D、(-1,0) |
已知数列{an}共有9项,其中a1=a9=1,且对每个i∈{1,2…,8},均有
∈{2,1,-
}|,记S=
+
+…+
,则S的最小值为( )
| ai+1 |
| ai |
| 1 |
| 2 |
| a2 |
| a1 |
| a3 |
| a2 |
| a9 |
| a8 |
| A、4 | B、6 | C、8 | D、10 |
已知正项等差数列{an}满足:an2-an+1-an-1=0(n≥2),等比数列{bn}满足:bn+1•bn-1-2bn=0(n≥2),则log2(an+bn)=( )
| A、-1或2 | B、0或2 | C、1 | D、2 |
 高三年上学期期末考试中,某班级数学成绩的频率分布直方图如图所示,数据分组依次如下:[70,90),[90,110),[100,130),[130,150),估计该班级数学成绩的平均分等于( )
高三年上学期期末考试中,某班级数学成绩的频率分布直方图如图所示,数据分组依次如下:[70,90),[90,110),[100,130),[130,150),估计该班级数学成绩的平均分等于( )| A、112 | B、114 |
| C、116 | D、120 |
下列函数f(x)中,满足“对任意x1,x2∈(-∞,0),当x1<x2时,都有f(x1)<f(x2)”的函数是( )
| A、f(x)=-x+1 |
| B、f(x)=x2-1 |
| C、f(x)=2x |
| D、f(x)=ln(-x) |