题目内容
关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的蒲丰实验，借鉴其原理，我们也可以采用计算机随机数模拟实验的方法来估计π的值：先由计算机产生1200对0～1之间的均匀随机数x，y；再统计两个数能与1构成钝角三角形三边的数对（x，y）的个数m；最后再根据统计数m来估计π的值，假如统计结果是m=940，那么可以估计π≈ （精确到0.001）
考点：模拟方法估计概率
专题：计算题,概率与统计
分析：由试验结果知1200对0～1之间的均匀随机数x，y，满足
，面积为1，两个数能与1构成钝角三角形三边的数对（x，y），满足x2+y2＜1且
，面积为
，由几何概型概率计算公式，得出所取的点在圆内的概率是圆的面积比正方形的面积，二者相等即可估计π的值．
|
|
| π |
| 4 |
解答：
解：由题意，1200对0～1之间的均匀随机数x，y，满足
，面积为1，
两个数能与1构成钝角三角形三边的数对（x，y），满足x2+y2＜1且
，面积为
，
因为共产生了1200对[0，1）内的随机数（x，y），其中能使x2+y2＜1的有m=940对，
所以
=
，所以π=3.133．
故答案为：3.133．
|
两个数能与1构成钝角三角形三边的数对（x，y），满足x2+y2＜1且
|
| π |
| 4 |
因为共产生了1200对[0，1）内的随机数（x，y），其中能使x2+y2＜1的有m=940对，
所以
| 940 |
| 1200 |
| π |
| 4 |
故答案为：3.133．
点评：本题考查了随机模拟法求圆周率的问题，也考查了几何概率的应用问题，是综合题．
练习册系列答案
考前必练系列答案
相关题目
已知正项等差数列{an}满足：an2-an+1-an-1=0（n≥2），等比数列{bn}满足：bn+1•bn-1-2bn=0（n≥2），则log2（an+bn）=（ ）
| A、-1或2 | B、0或2 | C、1 | D、2 |
从1，2，3，4，5这5个数中任取两数，其中：①恰有一个是偶数和恰有一个是奇数；②至少有一个是奇数和两个都是奇数；③至少有一个是奇数和两个都是偶数；④至少有一个是奇数和至少有一个是偶数． 上述事件中，是对立事件的是（ ）
| A、① | B、②④ | C、③ | D、①③ |
高三年上学期期末考试中，某班级数学成绩的频率分布直方图如图所示，数据分组依次如下：[70，90），[90，110），[100，130），[130，150），估计该班级数学成绩的平均分等于（ ）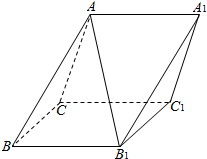
如图，在斜三棱柱ABC-A1B1C1中，侧面ACC1A1与侧面CBB1C1都是菱形，∠ACC1=∠CC1B1=60°，AC=2．