题目内容
若函数f(x)=sinωxcosωx+
sin2ωx-
(ω>0)的图象与直线y=m(m为常数)相切,并且切点的横坐标依次构成公差为π的等差数列.
(Ⅰ)求ω及m的值;
(Ⅱ)求函数y=f(x)在x∈[0,2π]上所有零点的和.
| 3 |
| ||
| 2 |
(Ⅰ)求ω及m的值;
(Ⅱ)求函数y=f(x)在x∈[0,2π]上所有零点的和.
考点:数列的求和,两角和与差的正弦函数,二倍角的正弦,二倍角的余弦
专题:等差数列与等比数列,三角函数的求值
分析:(Ⅰ)把f(x)=sinωxcosωx+
sin2ωx-
利用二倍角的余弦公式化简,然后由周期公式求周期;
(Ⅱ)由(Ⅰ)知f(x)=sin(2ωx-
),结合在x∈[0,2π]上的零点求得答案.
| 3 |
| ||
| 2 |
(Ⅱ)由(Ⅰ)知f(x)=sin(2ωx-
| π |
| 3 |
解答:
解:(Ⅰ)∵f(x)=sinωxcosωx+
sin2ωx-
=
sin2ωx+
(1-cos2ωx)-
=
sin2ωx-
cos2ωx=sin(2ωx-
),
依题意得函数f(x)的周期为π且ω>0,
∴2ω=
=2,
∴ω=1,则m=±1;
(Ⅱ)由(Ⅰ)知f(x)=sin(2ωx-
),∴2x-
=kπ(k∈Z),
∴x=
+
.
又∵x∈[0,2π],
∴x=
,
,
,
.
∴y=f(x)在x∈[0,2π]上所有零点的和为
+
+
+
=
.
| 3 |
| ||
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
依题意得函数f(x)的周期为π且ω>0,
∴2ω=
| 2π |
| π |
∴ω=1,则m=±1;
(Ⅱ)由(Ⅰ)知f(x)=sin(2ωx-
| π |
| 3 |
| π |
| 3 |
∴x=
| kπ |
| 2 |
| π |
| 6 |
又∵x∈[0,2π],
∴x=
| π |
| 6 |
| 2π |
| 3 |
| 7π |
| 6 |
| 5π |
| 3 |
∴y=f(x)在x∈[0,2π]上所有零点的和为
| π |
| 6 |
| 2π |
| 3 |
| 7π |
| 6 |
| 5π |
| 3 |
| 11π |
| 3 |
点评:本题主要考查三角函数两倍角公式、辅助角公式、等差数列公差、等差数列求和方法、函数零点基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归转化思想,是中档题.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的离心率为4,过右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于点H,若|MN|=10,则|HF|=( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、14 | B、16 | C、18 | D、20 |
某校开设A类课3门,B类课5门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有
( )
( )
| A、15种 | B、30种 |
| C、45种 | D、90种 |
已知正项等差数列{an}满足:an2-an+1-an-1=0(n≥2),等比数列{bn}满足:bn+1•bn-1-2bn=0(n≥2),则log2(an+bn)=( )
| A、-1或2 | B、0或2 | C、1 | D、2 |
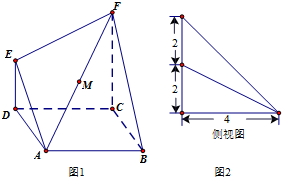 在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=
在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=