Question

如图，在△ABC中，若∠B=90°，∠ACD=45°，BC=3，BD=1，则AD=

 

．

Answer 1

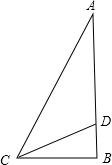
考点：解三角形

专题：解三角形

分析：根据三角函数的定义求出CD，以及sinA的值，利用两角和差的正弦公式和正弦定理即可得到结论．

解答： 解：∵若∠B=90°，∠ACD=45°，BC=3，BD=1，
∴CD=

BC2+BD2

=

9+1

=

10

，
设∠BDC=θ，则A=θ-45°，
∵sinθ=

BC

CD

=

3

10

，cosθ=

BD

CD

=

1

10

，
∴sinA=sin（θ-45°）=sinθcos45°-cosθsin45°=

3

10

×

2

2

-

1

10

×

2

2

=

5

5

，
在三角形ACD中，
由正弦定理得

AD

sin45°

=

CD

sinA

，
∴AD=

CD

sinA

•sin45°=

10

5 5

×

2

2

=5，
故答案为：5

点评：本题主要考查解三角形的应用，利用两角和差的正弦公式求出sinA以及利用正弦定理是解决本题的关键．