题目内容
6．方程（1+4k）x-（2-3k）y+2-14k=0所确定的直线必经过点（ ）| A． | （2，2） | B． | （-2，2） | C． | （-6，2） | D． | （3，-6） |
分析 方程（1+4k）x-（2-3k）y+2-14k=0化为：k（4x+3y-14）+（x-2y+2）=0，令$\left\{\begin{array}{l}{4x+3y-14=0}\\{x-2y+2=0}\end{array}\right.$，解出即可得出．
解答 解：方程（1+4k）x-（2-3k）y+2-14k=0化为：k（4x+3y-14）+（x-2y+2）=0，
令$\left\{\begin{array}{l}{4x+3y-14=0}\\{x-2y+2=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$．
因此方程所确定的直线必经过点（2，2）．
故选：A．
点评 本题考查了直线系的应用、方程组的解法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
19．已知p：?x＞0，ex-ax＜1成立，q：函数f（x）=-（a-1）x是减函数，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
14．
如图，一块长宽分别为30M、40M的矩形草地，其中间及四角是半径为10M的圆和扇形花圃，随意向草地浇水，则浇在花圃中的概率为（ ）
如图，一块长宽分别为30M、40M的矩形草地，其中间及四角是半径为10M的圆和扇形花圃，随意向草地浇水，则浇在花圃中的概率为（ ）| A． | $\frac{π}{12}$ | B． | $1-\frac{π}{6}$ | C． | $\frac{π}{6}$ | D． | $1-\frac{π}{12}$ |
1．若数据x1，x2，…，xn的平均值为$\overline x$，方差为S2，则3x1+5，3x2+5，…，3xn+5的平均值和方差分别为（ ）
| A． | $\overline{x}$和S2 | B． | 3$\overline{x}$+5和9S2 | C． | 3$\overline{x}$+5和S2 | D． | $\overline{x}$和9S2 |
11．设$\overrightarrow a=（1\;，\;2）\;，\;\overrightarrow b=（1\;，\;1）$，$\overrightarrow c=\overrightarrow a+k\overrightarrow b$，若$\overrightarrow b⊥\overrightarrow c$，则实数k=（ ）
| A． | $-\frac{3}{2}$ | B． | $-\frac{5}{3}$ | C． | $\frac{5}{3}$ | D． | $\frac{3}{2}$ |
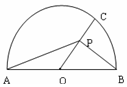如图，半圆的直径AB=4，O为圆心，C为半圆上不同A，B的任意一点，若P为半径OC上的动点，则（$\overrightarrow{PA}+\overline{PB}$）•$\overline{PC}$的最小值等于（ ）