题目内容
15.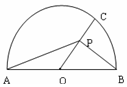 如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )
如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )| A. | 2 | B. | -1 | C. | -2 | D. | 0 |
分析 由O为AB的中点,得出$\overrightarrow{PA}$+$\overrightarrow{PB}$=2$\overrightarrow{PO}$,求出($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$=2$\overrightarrow{PO}$•$\overrightarrow{PC}$;由|$\overrightarrow{PO}$|+|$\overrightarrow{PC}$|=2为定值,求出($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值.
解答 解:因为O为AB的中点,
所以$\overrightarrow{PA}$+$\overrightarrow{PB}$=2$\overrightarrow{PO}$,
从而($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$=2$\overrightarrow{PO}$•$\overrightarrow{PC}$;
又|$\overrightarrow{PO}$|+|$\overrightarrow{PC}$|=2为定值,
所以当且仅当|$\overrightarrow{PO}$|=|$\overrightarrow{PC}$|=1,
即P为OC的中点时,($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$取得最小值是-2.
故选:C.
点评 本题考查了平面向量的数量积运算和基本不等式的应用问题,是基础题目.

| A. | 36 | B. | 40 | C. | 50 | D. | 52 |
| A. | (2,2) | B. | (-2,2) | C. | (-6,2) | D. | (3,-6) |
| A. | x=-$\sqrt{2}$ | B. | x=-4 | C. | x=-1 | D. | x=-8 |
| A. | 对分类变量x与y的随机变量k2的观测值k来说,k越小,判断“x与y有关系”的把握程度越大 | |
| B. | 两个随机变量的线性相关性越强,相关系数的绝对值越接近于0 | |
| C. | 若数据x1,x2,x3,…,xn的方差为1,则2x1,2x2,2x3,…,2xn的方差为2 | |
| D. | 在回归分析中,可用相关指数R2的值判断模型的拟合效果,R2越大,模型的拟合效果越好. |
| A. | {-1} | B. | {5,-1} | C. | {5} | D. | {-5,5,-1} |