题目内容
已知二次函数f(x)=ax2+bx.
(1)若函数f(x)的最小值为f(-1)=-1,F(x)=
,求F(x)的单调区间;
(2)若a=1,且f(x)≤1在区间(0,1]上恒成立,试求b的取值范围.
(1)若函数f(x)的最小值为f(-1)=-1,F(x)=
|
(2)若a=1,且f(x)≤1在区间(0,1]上恒成立,试求b的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)结合二次函数的性质得到方程组解出a,b的值即可;
(2)将问题转化为b≤-x+
在(0,1]恒成立,令g(x)=-x+
,得到g(x)在(0,1]递减,求出g(x)的最小值,从而求出b的范围.
(2)将问题转化为b≤-x+
| 1 |
| x |
| 1 |
| x |
解答:
解:(1)∵f(x)的最小值为f(-1)=-1,
∴
,解得:
,
∴f(x)=x2+2x,
∵F(x)=
,
∴F(x)=|f(x)|,
画出函数F(x)的图象,如图示:
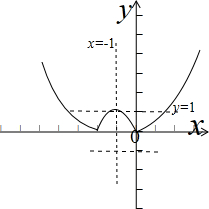 ,
,
∴F(x)在(-∞,-2)递减,在(-2,-1)递增,
在(-1,0)递减,在(0,+∞)递增;
(2)当a=1时,f(x)=x2+bx,
由f(x)≤1在区间(0,1]上恒成立,
得x2+bx-1≤0在(0,1]上恒成立,
即:b≤-x+
在(0,1]恒成立,
令g(x)=-x+
,则g′(x)=-1-
<0,
∴g(x)在(0,1]递减,∴g(x)min=g(1)=0,
∴b≤0.
∴
|
|
∴f(x)=x2+2x,
∵F(x)=
|
∴F(x)=|f(x)|,
画出函数F(x)的图象,如图示:
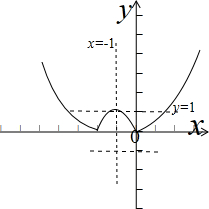 ,
,∴F(x)在(-∞,-2)递减,在(-2,-1)递增,
在(-1,0)递减,在(0,+∞)递增;
(2)当a=1时,f(x)=x2+bx,
由f(x)≤1在区间(0,1]上恒成立,
得x2+bx-1≤0在(0,1]上恒成立,
即:b≤-x+
| 1 |
| x |
令g(x)=-x+
| 1 |
| x |
| 1 |
| x2 |
∴g(x)在(0,1]递减,∴g(x)min=g(1)=0,
∴b≤0.
点评:本题考查了二次函数的性质,考查了函数恒成立问题,考查了转化思想,是一道中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
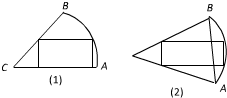 某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.
某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.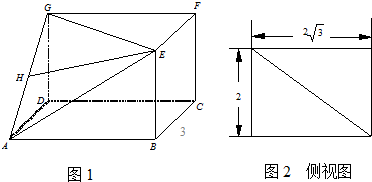
 函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<
函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<