题目内容
已知函数f（x）是定义在（-2，2）上的减函数，若f（m-1）＞f（2m-1），则实数m的取值范围为 ．
考点：函数单调性的性质
专题：函数的性质及应用
分析：由函数f（x）是定义在（-2，2）上的减函数，可将不等式f（m-1）＞f（2m-1）化为：-2＜m-1＜2m-1＜2，解得答案．
解答：
解：∵函数f（x）是定义在（-2，2）上的减函数，
∴不等式f（m-1）＞f（2m-1）可化为：
-2＜m-1＜2m-1＜2，
解得：m∈（0，
），
故答案为：（0，
）
∴不等式f（m-1）＞f（2m-1）可化为：
-2＜m-1＜2m-1＜2，
解得：m∈（0，
| 3 |
| 2 |
故答案为：（0，
| 3 |
| 2 |
点评：本题考查的知识点是函数单调性的应用，其中根据函数的单调性，将不等式化为：-2＜m-1＜2m-1＜2，是解答的关键．
练习册系列答案
相关题目
已知全集U=R，M={x|-3≤x＜5}，则∁uM=（ ）
| A、{x|x＜-3或x≥5} |
| B、{x|x≤-3或x＞5} |
| C、{x|x＜-3且x≥5} |
| D、{x|x≤-3且x＞5} |
下列条件中，可得出直线a∥平面α的是（ ）
| A、a与α内的两条相交直线不相交 |
| B、a与α内的所有直线都不相交 |
| C、a与α内的无数条直线不相交 |
| D、a与α内的无数条直线平行 |
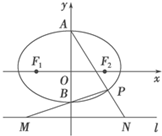如图，椭圆