��Ŀ����
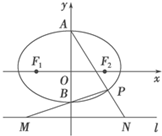 ��ͼ����Բ
��ͼ����Բ| x2 |
| a2 |
| y2 |
| b2 |
��P����Բ�����ڵ�A��B������һ�㣬����AP���ӳ���ֱ��l�ڵ�N������PB���ӳ���ֱ��l�ڵ�M����AP���ڵ�ֱ�ߵ�б��Ϊk1��BP���ڵ�ֱ�ߵ�б��Ϊk2������Բ��������Ϊ
| ||
| 2 |
��1����k1•k2��ֵ���߶�MN����Сֵ��
��2�����ŵ�P�ı仯����MNΪֱ����Բ�Ƿ������㣿�������㣬����ö��㣻�粻�����㣬��˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺������,ֱ����Բ,Բ���ߵĶ��塢�����뷽��
��������1���������֪e=
=
��b=1����a2-b2=c2�����a��b�õ���Բ���̣�����Բ�ϵ�P��x0��y0����������Բ���̣�����б�ʹ�ʽ�����ɵõ�k1•k2��ֵ����M��x1��-2����N��x2��-2�������x1x2=-12�����ɻ�������ʽ���MN=|x1-x2|����Сֵ��
��2����M��x1��-2����N��x2��-2��������MNΪֱ����Բ�ķ���Ϊ��x-x1����x-x2��+��y+2��2=0��������������Բ�����㣬����x=0��x2+��y+2��2-12=0����������жϣ�
| c |
| a |
| ||
| 2 |
��2����M��x1��-2����N��x2��-2��������MNΪֱ����Բ�ķ���Ϊ��x-x1����x-x2��+��y+2��2=0��������������Բ�����㣬����x=0��x2+��y+2��2-12=0����������жϣ�
���
�⣺��1����Ϊe=
=
��b=1����a2-b2=c2�����a=2��
������ԲC�ı�����Ϊ
+y2=1��
����Բ�ϵ�P��x0��y0������
+y02=1��
����k1•k2=
•
=
=-
��
��ΪM��N��ֱ��l��y=-2�ϣ���M��x1��-2����N��x2��-2����
�ɷ���֪
+y2=1֪��A��0��1����B��0��-1����
����KBM•kAN=
•
=
��
��������֪kAN•kBM=k1•k2=-
������x1x2=-12��
������x1��0����x2��0����
MN=|x1-x2|=x2-x1=x2+
��2
=4
��
���Ե��ҽ���x2=-x1=2
ʱ��MNȡ����Сֵ4
��
��2����M��x1��-2����N��x2��-2����
����MNΪֱ����Բ�ķ���Ϊ
��x-x1����x-x2��+��y+2��2=0��
��x2+��y+2��2-12-��x1+x2��x=0����Բ�����㣬
����x=0��x2+��y+2��2-12=0�����x=0��y=-2��2
��
���ԣ����۵�P��α仯����MNΪֱ����Բ������㣨0��-2��2
����
| c |
| a |
| ||
| 2 |
������ԲC�ı�����Ϊ
| x2 |
| 4 |
����Բ�ϵ�P��x0��y0������
| x02 |
| 4 |

����k1•k2=
| y0-1 |
| x0 |
| y0+1 |
| x0 |
| y02-1 |
| x02 |
| 1 |
| 4 |
��ΪM��N��ֱ��l��y=-2�ϣ���M��x1��-2����N��x2��-2����
�ɷ���֪
| x2 |
| 4 |
����KBM•kAN=
| -2-(-1) |
| x1-0 |
| -2-1 |
| x2-0 |
| 3 |
| x1x2 |
��������֪kAN•kBM=k1•k2=-
| 1 |
| 4 |
������x1��0����x2��0����
MN=|x1-x2|=x2-x1=x2+
| 12 |
| x2 |
x2•
|
| 3 |
���Ե��ҽ���x2=-x1=2
| 3 |
| 3 |
��2����M��x1��-2����N��x2��-2����
����MNΪֱ����Բ�ķ���Ϊ
��x-x1����x-x2��+��y+2��2=0��
��x2+��y+2��2-12-��x1+x2��x=0����Բ�����㣬
����x=0��x2+��y+2��2-12=0�����x=0��y=-2��2
| 3 |
���ԣ����۵�P��α仯����MNΪֱ����Բ������㣨0��-2��2
| 3 |
���������⿼����Բ�ķ��̺����ʣ�Բ�ķ��̵�������ֱ�ߵ�б�ʹ�ʽ�����ã��Լ�����������⣬����ͻ��������������е��⣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
���ABC���ڽ�A��B��C���Եı�a��b��c�ɵȱ����У���
��ȡֵ��Χ�ǣ�������
| sinA+cosA•tanC |
| sinB+cosB•tanC |
| A����0��+�ޣ� | ||||||||
B����0��
| ||||||||
C����
| ||||||||
D����
|
P����Բ
+
=1��һ�㣬F1��F2�ֱ�Ϊ���ҽ��㣬��PF1F2������Բ�İ뾶Ϊ1����|
+
|��ֵΪ��������
| x2 |
| 25 |
| y2 |
| 9 |
| PF1 |
| PF2 |
| A��8 | ||||
B��4
| ||||
| C��4 | ||||
D��
|
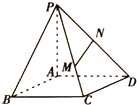 ��ͼ��ʾ����֪����ABCD��PΪƽ��ABCD��һ�㣬��PA����ABCD��M��N�ֱ�ΪPC��PD�ϵĵ㣬��PM��MC=2��1��NΪPD���е㣬������
��ͼ��ʾ����֪����ABCD��PΪƽ��ABCD��һ�㣬��PA����ABCD��M��N�ֱ�ΪPC��PD�ϵĵ㣬��PM��MC=2��1��NΪPD���е㣬������